중요했던 부분:
- uv
uv는 primitive상에서 가로값과 세로값을 1로써 비율을 맞추었을때 그 비율을 알려준다. 아래의 그림을 하나의 프리미티브라고 가정하고 가로값을 v 세로값을 u이라고 가정했을때 (top view에서 본 Grid기준) 만약 u값이 0.7이고 v값이 0.2라면 아래의 그림처럼 빨간색 점 부분을 가리킬 것이다.

- primuv(): Primitive UV Function
primuv()는 원하는 특정 primitive에서 primitive의 u값과 v값을 토대로 원하는 정보를 받아와주는 Function이다. primuv()에는 wrangle노드에 연결된 input의 넘버, 어떠한 정보를 불러오고자 하는지, 몇번 primitive, 그리고 uv를 vector값으로 입력해주어야 한다.
// chv()으로 UV라는 파라미터를 만들어 조절한 값을 vector variable uv에 저장하여라
vector uv = chv ("UV");
/* primuv()을 활용하여 1번 인풋으로 들어온 geometry의 0번 프리미티브의 uv값에 해당하는 Vector값의 포지션값을
불러와 vector variable new에 저장하여라*/
vector new = primuv (1, "P", 0, uv);
// 방금전 선언한 vector variable new 값을 @P로 보여줌
@P = new;
/* primuv()을 활용하여 1번 인풋으로 들어온 geometry의 0번 프리미티브의 uv값에 해당하는 Vector값의 노멀값을
불러와 vector attribute @N에 저장하여라*/
@N = primuv (1, "N", 0, uv);이때 아래와 같은 노드를 구성해주어 grid가 transform으로 움직이게 만들어서 같이 wrangle노드에 연결된 포인트가 유저가 파라미터로 지정한 uv의 위치에서 grid의 모션과 동일하게 나오게 해준다. 그때 copy to points로 연결된 rubbertoy가 포인트의 위치에 카피될수 있도록 하고 이들을 grid와 merge로 묶어서 rubbertoy가 grid의 모션에 둥둥 떠나니게끔 세팅하였다. 이때 @P는 포인트의 위치라 유저가 grid상에서 rubbertoy가 어디 위치해 있을지 결정해주고 @N는 노멀값이라 grid가 움직일때 rubbertoy도 grid가 움직일때의 방향과 동일하게끔 향하게끔 설정하였다. 이때 rubbertoy가 배까고 누워있는 것을 볼 수 있는데 이는 grid의 normal값이 (0, 1, 0)인데 rubbertoy의 노멀값을 동일하게 설정하면 배까고 누워있게 된다. 이를 보완하기 위해 transform을 rubbertoy에 연결해 rotation값의 x값을 90도 돌려주었다.
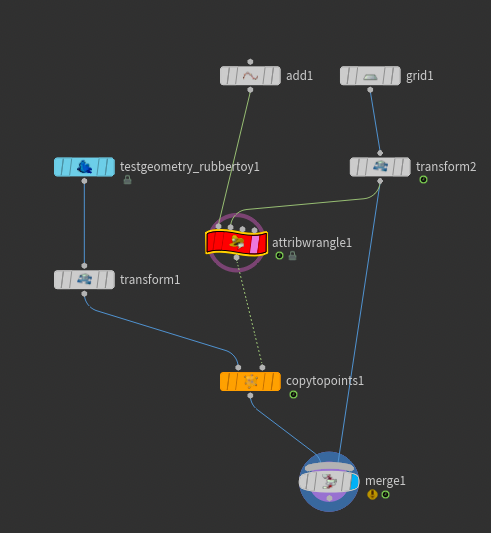
이때 rubbertoy를 grid상에서 뺑글뺑글 돌리고 하고 싶을땐 어떻게 해야 할까? 이는 wrangle노드 안에 있는 vex를 새롭게 고침으로써 가능한데 이는 이와 같이 코드로 작성해줄 수 있다.
// vector variable uv선언
vector uv;
// 이는 본격적으로 geometry가 원운동을 하게끔 만듦
// vector variable uv에서 x값을 sine 파형으로 시간이 지날수록 움직이게끔설정
uv.x = sin (@Time);
// vector variable uv에서 y값을 cosine 파형으로 시간이 지날수록 움직이게끔설정
uv.y = cos (@Time);
/* 이때 uv값에 fit()을 사용하여 기존에 -1과 1사이에 있던 파형의 range를 -0.2와 0.2사이로 바꾸어
원운동의 반경을 줄임*/
uv = fit (uv, -1, 1, -0.2, 0.2);
/* 이때 uv값에 아래와 같은 vector값을 더하여 가로로 중심 세로로 중심으로 이동시켜 grid의 중심을
기준으로 원운동을하게끔 설정*/
uv += {0.5, 0.5, 0};
/* primuv()을 활용하여 1번 인풋으로 들어온 geometry의 0번 프리미티브의 uv값에 해당하는 Vector값의 포인트 위치값을
불러와 vector attribute @P에 저장하여라*/
@P = primuv (1, "P", 0, uv);
/* primuv()을 활용하여 1번 인풋으로 들어온 geometry의 0번 프리미티브의 uv값에 해당하는 Vector값의 노멀값을
불러와 vector attribute @N에 저장하여라*/
@N = primuv (1, "N", 0, uv);그러면 위와는 다르게 원운동을 하면서와 동시의 grid의 포지션값과 노멀값을 따라가는 것을 볼 수 있다.
이때 더욱 grid를 화려하게끔 꾸며주고 싶다면 mountain노드를 연결하여 울퉁불퉁하게 만드는 것이 가능하다. 이때 grid를 transform으로 rotation시켜주던것과 같이 mountain의 offset값을 $F으로 프레임이 흐를수록 모양이 바뀌게 만들어 동적인 모션이 가능케끔 하였다.이때 vex 코드도 위와 동일하게 작성하여 원운동을 하면서 grid의 normal값과 포인트 위치값을 따라가게끔 만들었고 이는 rubbertoy가 울퉁불퉁한 표면위에서 우당탕탕 하는 것 같은 모션을 만들어 보았다.
// vector variable uv선언
vector uv;
// 이는 본격적으로 geometry가 원운동을 하게끔 만듦
// vector variable uv에서 x값을 sine 파형으로 시간이 지날수록 움직이게끔설정
uv.x = sin (@Time);
// vector variable uv에서 y값을 cosine 파형으로 시간이 지날수록 움직이게끔설정
uv.y = cos (@Time);
/* 이때 uv값에 fit()을 사용하여 기존에 -1과 1사이에 있던 파형의 range를 -0.2와 0.2사이로 바꾸어
원운동의 반경을 줄임*/
uv = fit (uv, -1, 1, -0.2, 0.2);
/* 이때 uv값에 아래와 같은 vector값을 더하여 가로로 중심 세로로 중심으로 이동시켜 grid의 중심을
기준으로 원운동을하게끔 설정*/
uv += {0.5, 0.5, 0};
/* primuv()을 활용하여 1번 인풋으로 들어온 geometry의 0번 프리미티브의 uv값에 해당하는 Vector값의 포인트 위치값을
불러와 vector attribute @P에 저장하여라*/
@P = primuv (1, "P", 0, uv);
/* primuv()을 활용하여 1번 인풋으로 들어온 geometry의 0번 프리미티브의 uv값에 해당하는 Vector값의 노멀값을
불러와 vector attribute @N에 저장하여라*/
@N = primuv (1, "N", 0, uv);
이때 grid값의 row와 column을 올리면 rubbertoy가 전체적인 곳이 아닌 하나의 프리미티브 상에서 움직이게 되는데 이는 uv특성상 하나의 프리미티브를 기준으로 uv값을 계산하기 때문이다. 이를 방지하려면 grid의 타입을 Polygon이 아닌 NURBS로 바꾸어주면 grid의 프리미티브가 하나만으로 구성되어져 전체적으로 rubbertoy가 움직이게 되는 것을 알 수 있다
위에서 설명한것 처럼 uv값은 오직 하나의 프리미티브를 가로세로 값으로 비율을 계산하여 생성되는데 이는 이와 같은 실험으로도 알 수 있었다. grid에 scatter을 연결하여 포인트들로 만든 후에 scatter의 output attribute 메뉴로 가 Prim UVW Attribute로 가 Cd 색깔값으로 설정해주면 프리미티브 상에서 아래로 갈수록 uv vector상 (1, 0, 0)값이 강해지고 오른쪽으로 갈 수록 uv vector상 (0, 1, 0)값이 강해져 각각 색깔값 (RGB)의 맞게 빨간색 그리고 초록색을 띄는 것을 알 수 있었다.

이를 많은 삼각형으로 이루어진 sphere에다 적용하면 이와 같은 모양이 나오는데 이도 동일하게 각각의 uv값에 알맞게 @Cd 색깔값들이 형성된것을 알 수 있다. 이때 만약 rubbertoy에 원운동을 시킨다면 프리미티브 하나가 아닌 두개의 삼각형으로 이루어진 평행사변형위에서 찌그러진 모양을 하여 원운동을 하게 된다는 사실을 알 수 있었다.

이와 같이 line 포인트들로 이루어진 선에다 적용해도 오른쪽으로 갈수록 uv vector 상 v의 결과가 없음으로 u값만 진행되어 (1, 0, 0)이 오른쪽으로 갈수록 짙어져 빨개지는 것을 알 수 있다.

이때 primitive sphere에다 동일한 과정을 또 적용하면 uv값의 따라 색상이 알맞게 표현되어 이와 같은 쉐입을 띄는 것을 알수 있다. 이로인해 알수 있는 사실은 아까 만들었던 면위에서 원운동을 만든다라는 방식이 모든 표면에서 다일어나는 것은 아니라는 것을 알 수 있다. 그래소 primuv()상에서 세번째 정보 (몇번 프리미티브에서) uv값을 받아올지에 대해 정확하게 쓰는 것이 중요하다.

- xyzdist(): XYZ Distance Function
xyzdist()는 minpos()/nearpoint()/nearpoints() 와 비슷하게 하나의 geometry에서 가장 가까운 geometry의 대한 정보를 가져다 주는데 세개의 정보를 가져다 준다. 이는 float값인 두 geometry의 사이의 거리값, 그리고 가장 가까운 프리미티브가 몇번인지 (integer value), 그리고 가장 가까운 부분의 uv값이 어떤 값인지 vector값으로 가져와 준다. 이때 xyzdist()에는 네개의 값을 입력해주는데 wrangle의 몇번 인풋에 연결되었는지, 어떤 Attribute정보를 불러오고 싶은지, 어떤 프리미티브 값을 불러오고 싶은지, 그리고 uv값을 뭘 불러오고 싶인지 입력해야 한다. xyzdist()는 특이한 부분이 있는데 지금까지 " "을 사용하여 attribute선언 없이 곧바로 집어넣을 수 있었지만 xyzdist()는 attribute을 정보로써 입력할때 미리 type casting을 해주어야 하는 사실을 알았다. 이는 간단하게 수치를 저장할 필요없이 type casting으로 선언만 해주면된다. 그래서 나는 아래와 같이 식을 작성해보았다.
우선 다음과 같이 포인트와 box를 만들어 주어 포인트로부터 box를 이루는 포인트 위치들중 가장 가까운 포인트의 위치는 뭔지 구하기 위해 아래와 같이 노드를 구성해보았다.

// xyzdist()에 입력할 정보들을 미리 type casting을 해주어 선언해주었다.
f@dist; // 가장 가까운 포인트 위치까지의 거리
i@primid; // 가장 가까운 포인트가 위치해있는 프리미티브 넘버
v@uv; // 가장 가까운 포인트 위치의 uv값
/* 0번 인풋으로 연결된 geometry로부터 1번 인풋으로 연결된 Geometry를 구성하는
점들중 방금전 설명한 세개의 값들을 불러와라. 이때 float @dist에는 가장 가까운 포인트 위치까지의 거리를 저장하여라*/
@dist = xyzdist (1, @P, @primid, @uv);
/* 이때 primuv()를 활용하여 1번 인풋으로 연결된 Geometry에 @primid (가장 가까운 프리미티브)에 해당하는 프리미티브
안에 있는 uv에 해당하는 포인트의 위치값을 가져와 vector varible new에 저장*/
vector new = primuv (1, "P", @primid, @uv);
/* 0번 인풋으로 연결된 geometry로부터 1번 인풋으로 연결된 Geometry를 구성하는
점들중 방금전 설명한 세개의 값들을 불러와라. 이때 float 0번 인풋geometry의 @Cd에는
가장 가까운 포인트의 색깔값을 저장하여라*/
@Cd = primuv (1, "Cd", @primid, @uv);
// 그 uv값에 해당하는 포인트를 생성해주어라
addpoint (0, new);
xyzdist()와 primuv()을 둘 다 사용하여 Day7때 nearpoint()를 배웠을때 처럼 grid를 구역별로 나뉘어 색깔을 알맞게 칠해줄 수 있다. 우선 아래와 같이 grid를 scatter로 점들로 흩어지게끔 만든다음 copytopoints로 sphere로 점들의 위치에 카피하여 attribute randomize로 sphere의 색깔을 다채롭게 정해주었다. 그다음 wrangle노드로 grid를 0번 인풋으로 연결하고 sphere들이 있는 노드를 1번 인풋에 연결하여 grid를 이루는 프리미티브들이 각각 가장 가까운 sphere의 색상과 동일하게 색을 이루도록 설정하도록 하였다.

// xyzdist()에 입력할 정보들을 미리 type casting을 해주어 선언해주었다.
f@dist; // 가장 가까운 포인트 위치까지의 거리
i@id; // 가장 가까운 포인트가 위치해있는 프리미티브 넘버
v@uv; // 가장 가까운 포인트 위치의 uv값
/* 0번 인풋으로 연결된 geometry로부터 1번 인풋으로 연결된 Geometry를 구성하는
sphere들중 가장 가까운 sphere까지의 위치까지의 거리를 저장하여라*/
@dist = xyzdist (1, @P, @id, @uv);
/* 0번 인풋으로 연결된 geometry로부터 1번 인풋으로 연결된 Geometry를 구성하는
점들중 방금전 설명한 세개의 값들을 불러와라. 이때 각각의 grid를 구성하는 프리미티브의 @Cd값은
가장 가까운 sphere의 색깔값을 저장하여라*/
@Cd = primuv (1, "Cd", @id, @uv);
Exercises:
1. Use modulo with time to animate the uv vector you feed to primuv to have shapes smoothly slide across a single poly grid
우선 이문제는 기존에 grid에서 rubbertoy가 grid를 중심으로 원운동을했는데 uv값에 @Time을 더해주어 프레임이 흐를수록 rubbertoy가 uvw vector상 (1, 1, 1)에 위치해 있는 꼭짓점으로 슬라이드할 수 있게 해준 다음 문제에도 나와있듯이 float constant를 modulo해주어 반복되게끔 해주었다.
// vector variable uv선언
vector uv;
// 이는 본격적으로 geometry가 원운동을 하게끔 만듦
// vector variable uv에서 x값을 sine 파형으로 시간이 지날수록 움직이게끔설정
uv.x = sin (@Time);
// vector variable uv에서 y값을 cosine 파형으로 시간이 지날수록 움직이게끔설정
uv.y = cos (@Time);
/* 이때 uv값에 fit()을 사용하여 기존에 -1과 1사이에 있던 파형의 range를 -0.2와 0.2사이로 바꾸어
원운동의 반경을 줄임*/
uv = fit (uv, -1, 1, -0.2, 0.2);
/* 이때 uv값에 아래와 같은 vector값을 더하여 가로로 중심 세로로 중심으로 이동시켜 grid의 중심을
기준으로 원운동을하게끔 설정*/
uv += {0.5, 0.5, 0};
/* uv값에 @Time을 더하여 프레임이 흐를수록 uv값이 올라가 rubbertoy가 꼭짓점을 향하게 함과 동시에 유저가 파라미터
로 정한 float값을 modulo해주어 슬라이드 모션이 반복되게 만든다*/
uv += @Time*chf ("SPEED")%chf ("MODULO");
/* primuv()을 활용하여 1번 인풋으로 들어온 geometry의 0번 프리미티브의 uv값에 해당하는 Vector값의 포인트 위치값을
불러와 vector attribute @P에 저장하여라*/
@P = primuv (1, "P", 0, uv);
/* primuv()을 활용하여 1번 인풋으로 들어온 geometry의 0번 프리미티브의 uv값에 해당하는 Vector값의 노멀값을
불러와 vector attribute @N에 저장하여라*/
@N = primuv (1, "N", 0, uv);
2. Find the example on this site of using attrib interpolate with a scatter sop, see how similar it is to the primuv trick
primuv()의 기본적인 원리는 원하는 특정 프리미티브에서 프리미티브의 u값과 v값을 토대로 원하는 정보를 받아와 주는 function이다. 이때 scatter 노드를 활용하여 geometry를 모두 점으로 만들어 준뒤 이를 @Cd값으로 보여주어 각기 점에 해당하는 uv값에 맞게 동일한 색깔값을 형성하는 것을 볼 수 있었다. primuv()도 이와 마찬가지로 하나의 프리미티브 안에서 uv값을 기반으로 포인트의 위치나 색깔값을 정해줌으로 매우 비슷하게 작용한다는 것을 알 수 있다. 하지만 이때 grid가 아닌 입체적인 Geometry를 이용할때 즉 polygon sphere같은 geometry에서는 두 프리미티브를 가지고 평행사변형을 형성하여 그 부분에 uv값이 전체적으로 적용되어질 수 있다는 것이다. 그러므로 이때 유의해야 할점으로는 아까 만들었던 면위에서 원운동을 만든다라는 방식이 모든 표면에서 다일어나는 것은 아니라는 것을 알 수 있다 라는 사실이다.
3. Try primuv with curves/polylines, see if you can push points along a curve, see how you might use it for a simple crowd system
4. Using the above, how would you get cars to properly orient themselves on the curve? The lazy way is to use a trail sop, set it to calculate @v, and if there's no other @N/@up/@orient attribs, will point the copied geo along @v, but how would you then convert @v to @orient so its a stable rotation? There's hints elsewhere on the wiki for this, but see if you can work this out yourself.
이해가 안되었던 부분:
- Exercieses에서 3번과 4번 문제가 이해가 되지 않았다. primuv()을 curves와 polylines과 함께 사용하라는데 정확한 어떤의미인지 알수 없었다. 내가 아는 polyline은 면으로써 closed가 되지않은 프리미티브의 상태를 나타내는것으로 아는데 이를 사용하여 어떻게 커브를 따라 포인트들을 밀어내는지 simple crowd system을 생성하는지 어려웠다. 그리고 커브에 있는 car가 어떻게 하여 직접 자신의 rotation 방향을 조절하게끔 할 수 있는지 너무 어려웠다. 갑자기 exercises의 난이도가 확 올라간 느낌이라 정신이 얼얼하였다.
공부하면서 들었던 생각:
드디어 마지막에서 두번째 강의가 끝났다. 이제 오직 하나의 강의를 남겨두니 마음이 뭔가 이상하기도 하다. 마지막 exercises 두 문제를 풀지 못하여 조금 마음이 찝찝하긴 하지만 나중에 시간 많을때 다시 풀어야 겠다는 생각이 든다. Day 19는 생각보다 어려웠던 것 같다. 마지막 이라고 방심하지 말라는 CGwiki님의 뜻이라고 해석해야겠다. 그래도 거의 끝나가니 후련하기도 하고 미련이 남는 exercises들이 기억에 남기도 하다. 그런 Exercises들은 볼드체로 표기해놔서 나중에 다시 한번 풀어야 겠다는 생각이 든다. 이제 남은것은 Day 20, 복습일기, 기말과제 그리고 소감문만 남은 것 같다. 기말과제가 조금 어려울 것 같지만 지금까지 배웠던 방식을 통해서 할 수 있을때 까지 도전해봐야 겠다. Joy of Vex를 지금까지 해보면서 느낀점은 정말 후디니를 배우는 데 있어서 끝은 없는 것 같다. 아마 평생동안 배워야 하는 마음가짐으로 있어야 발전하겠다는 생각이 든다. 그래서 코스를 완주하고도 방심하지 말고 지금까지 배웠던 것을 상기하며 복습하며 공부해야겠다.
'FX > Houdini_Joy of VEX' 카테고리의 다른 글
| Joy of Vex - Assignment #2 & Final Review (2) | 2022.08.12 |
|---|---|
| Joy of Vex - Day 20: pointclouds, further learning (0) | 2022.08.07 |
| Joy of Vex - Day 18: intrinsics (0) | 2022.08.03 |
| Joy of Vex - Day 17-2: copy sop, orient, quaternions (0) | 2022.07.31 |
| Joy of Vex - Recap of Week 5 (0) | 2022.07.29 |