중요했던 부분:
- 심화적인 nearpoint() 복습
nearpoint()는 0번 wrangle input에 연결된 geometry로부터 1번 wrangle input으로 연결된 geometry를 구성하는 point들중 제일 가까운 point의 포인트 넘버를 반환하는 function이다.
int pt = nearpoint (1, @P);
/* 0번 인풋으로 연결된 geometry로부터 1번 인풋으로 연결된 Geometry를 구성하는 point들중 가장 가까운
점들을 찾아 그것들의 포인트 넘버를 반환하여 integer variable pt에 저장하여라*/
i@pt = pt; // integer variable pt를 attribute으로써도 나타내어라아래와 같이 Houdini상에서 1000개의 포인트를 가진 라인을 만들어주고 wrangle node의 0번 인풋에 연결하고 위의 빨간색 숫자에 해당하는 포인트들을 담당하는 geometry를 wrangle node의 1번 인풋에 연결해 주어 윗 식을 지정해주면...

1000개의 포인트들중 각기 자신의 위치를 기준으로 가장 가까운 빨간색 숫자가 할당된 포인트를 찾아 자신의 pt값을 저장한다.
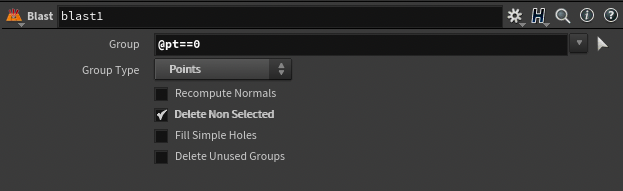
- blast (Group)
아랫 사진과 같이 blast node의 있는 group을 통해 Attribute @pt가 0일 경우의 포인트들만 보여주게 하거나 사라지게 할 수 있다. 윗 사진에서 아래 blast node를 통해 @pt값이 0인 포인트들만 나오게끔 실행하게 된다면 아래와 같이 나올 것 이다.

윗 blast노드를 각기 빨간색 포인트 넘버가 할당된 (즉 세 점)에 모두 입력하여 이렇게 계산된 결과에 아랫 코드를 입력하여 높이값으로 나타내주면 다음과 같은 결과가 나타난다.
i@pt; // cast type을 확실히 하기 위해 i@pt값을 따로 선언해서 불러와줌
/* 1번 포인트로 연결된 Geometry의 @pt값의 포인트 넘버 (nearpoint()로 생성된 attribute))에 (이 상황에선
모든 포인트 넘버) 해당하는 @P 포인트 위치값을 불러와 vector variable getPos에 저장하여라*/
vector getPos = point (1, "P", @pt);
/* 방금 전 선언한 1번 인풋으로 연결된 geometry의 포인트중 각기 가장 가까운 포인트들과 0번 인풋으로 연결된 모든
포인트들의 거리 길이 값을 Float variable d 에 저장하여라*/
float d = distance (@P, getPos);
// 방금 전 선언한 길이 거리 값을 float attribute d에 저장하여 geometry spreadsheet에 디스플레이
f@d = d;
// 방금 전 선언한 길이 거리 값을 @P.y 높이값으로 보여주어라
@P.y = d;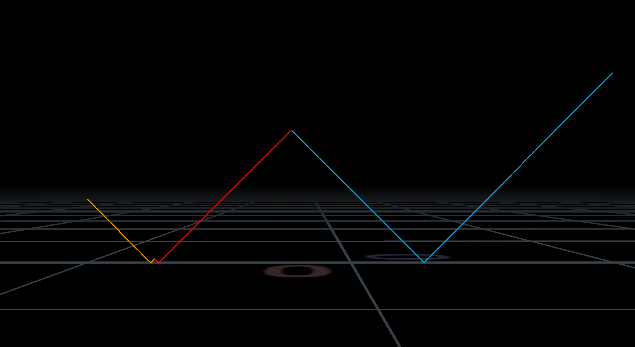
이를 한번에 해결하면 이렇게 된다. 이는 방금 전 코드가 따로따로 진행해줬다는것을 비교해 보았을때 오로지 한 wrangle node안에서 코드를 쓰면서 해결한다.
/* 0번 인풋으로 들어운 geometry의 모든 포인트들로부터 1번 인풋으로 들어온 geometry의
가장 가까운 포인트들의 포인트 넘버를 int variable pt에 저장하여라*/
// 점이 여러개 있을시 pt는 모든 포인트들의 위치에 따라 각기 달라진다
// 가져온 결과 point number 즉 @ptnum임
int pt = nearpoint (1, @P);
/* 1번 인풋으로 연결된 geometry에 pt값에 해당하는 point number를 가진 포인트들의 위치값을 가져와
vector variable getPos에 저장하여라*/
/* 가져온 결과 position 즉 @P임. 아까구한 int variable pt에 해당하는 포인트들의 수치값을
위치값으로 바꿨다고 생각하면 이해가 편함*/
vector getPos = point (1, "P", pt);
// 0번 인풋으로 들어온 Geometry를 구성하는 모든 포인트들과 방금 전 저장한 1번 geometry에 Pt값에 해당하는
포인트들의 위치값들 사이의 거리 길이를 구하여 float variable d에 저장하여라*/
float d = distance (@P, getPos);
// 그 모든 거리값을 @P.y 높이 값으로 보여주어라
@P.y = d;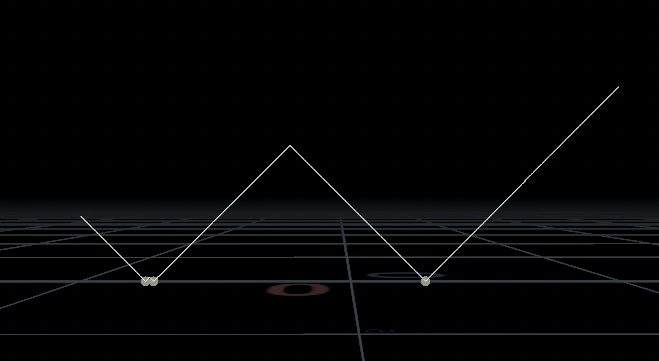
이를 활용하여 색다른 파형을 구축하여 모션을 줄 수 도 있다.
/* 0번 인풋으로 들어운 geometry의 모든 포인트들로부터 1번 인풋으로 들어온 geometry의
가장 가까운 포인트들의 포인트 넘버를 int variable pt에 저장하여라*/
// 점이 여러개 있을시 pt는 모든 포인트들의 위치에 따라 각기 달라진다
// 가져온 결과 point number 즉 @ptnum임
int pt = nearpoint (1, @P);
/* * 변수 생성 & 효과 생성 * */
// 여기 float variable fx는 전체적인 effect를 추가한 값임. 모든 효과에 대해 정의를 내려준다.
float fx = 0;
// 여기 float variables은 fx에 추가될 수치들로써 각기 어떠한 효과를 나타낼지 정의를 내려준다.
float fxA = 0;
// 방금 전 1번 인풋으로 연결된 pt에 포인트 넘버가 할당된 포인트들의 위치값을 vector variable getPos에 저장
vector getPos = point (1, "P", pt);
v@getPos = getPos; // 저장한 vector variable getPos를 attribute로써 나타내어라
/* 0번 인풋으로 들어온 Geometry를 구성하는 모든 포인트들과 방금 전 저장한 1번 geometry에 Pt값에 해당하는
포인트들의 위치값들 사이의 거리 길이를 구하여 float variable d에 저장하여라*/
float d = distance (@P, getPos);
// 여기 float variables은 fx에 추가될 수치들로써 각기 어떠한 효과를 나타낼지 정의를 내려준다.
/* 거리 길이값을 effect fxA에 적용함으로써 1번 인풋 geometry를 구성하는 포인트들을 기점으로 0번
인풋 geometry를 구성하는 모든 점들의 거리길이를 fxA에 저장한다.*/
fxA = d;
// @Time을 빼주어 움직이는 모션을 취해준다. 빼줌으로써 중심으로부터 바깥으로 빠져나가는 형태의 모션 구축
fxA -= @Time;
/* effect값에 floor()을 적용하여 내림을 취함으로써 높이값으로 나타내었을때 계단같은 형상이 나타나도록 유도
하지만 그 값을 전체 fxA에서 다시 빼서 반복되는 ramp가 나타나는 것처럼 쉐입을 생성하였다*/
fxA = fxA - floor (fxA);
/* 이때 fit()을 활용하여 쉐입을 뒤집어 버렸다. 이는 나중에 chramp()를 적용하였을때 모션이 진행될때
ramp가 x값으로 봤을때 0에서부터 1까지 나타나게 하기 위함이다.*/
fxA = fit (fxA, 0, 1, 1, 0);
fxA = chramp ("FXA", fxA); // chramp()을 통해 파형의 모양을 형성하였다
///* * 효과를 택 * */
/* 맨 위에 선언한 float variable fx에 모든 effect 변수와 ramp변수들을 차례대로 추가하여 fx를 순차적으로
업데이트 해주었다.*/
fx += fxA;
/* * 원본에 저장 * */
/* 방금 전 추가해준 모든 ramp안에 지정된 수치값에 따라 반영된 effect들을 포함하는 float variable fx를
@P.y 높이값으로 보여주어라*/
@P.y += fx;
/* 각각의 1번 인풋 geometry의 포인트 넘버에 rand()를 활용하여 random값으로 지정된 @Cd 컬러값을 적용하여
색으로써 구분가게끔 하여라*/
@Cd = rand (pt+333);
- pow(): Power Function
수에 제곱을 해준다. input으로는 제곱을 하려는 지수 수치를 입력해준다.
- Ripple Effect
방금 전 공부해본 여러가지 effect들과 nearpoint()의 특성을 활용하여 grid에 접목해 마치 물방울이 떨어지는 스타일의 모션을 만들어 보았다.
/* * 변수 생성 & 효과 생성 * */
// 여기 float variable fx는 전체적인 effect를 추가한 값임. 모든 효과에 대해 정의를 내려준다.
float fx = 0;
// 여기 float variables은 fx에 추가될 수치들로써 각기 어떠한 효과를 나타낼지 정의를 내려준다.
float fxA = 0;
// 방금 전 1번 인풋으로 연결된 0번 포인트 넘버가 할당된 포인트들의 위치값을 vector variable hitPos에 저장
vector hitPos = point (1, "P", 0);
/* 0번 인풋으로 들어온 Geometry를 구성하는 모든 포인트들과 방금 전 저장한 1번 geometry에 Pt값에 해당하는
포인트들의 위치값들 사이의 거리 길이를 구하여 float variable dist에 저장하여라*/
float dist = distance (@P, hitPos);
// 여기 float variables은 fx에 추가될 수치들로써 각기 어떠한 효과를 나타낼지 정의를 내려준다.
/* 거리 길이값을 effect fxA에 적용함으로써 1번 인풋 geometry를 구성하는 포인트들을 기점으로 0번
인풋 geometry를 구성하는 모든 점들의 거리길이를 fxA에 저장한다.*/
fxA = dist;
// @Time을 빼주어 움직이는 모션을 취해준다. 빼줌으로써 중심으로부터 바깥으로 빠져나가는 형태의 모션 구축
fxA -= @Time;
/* effect값에 floor()을 적용하여 내림을 취함으로써 높이값으로 나타내었을때 계단같은 형상이 나타나도록 유도
하지만 그 값을 전체 fxA에서 다시 빼서 반복되는 ramp가 나타나는 것처럼 쉐입을 생성하였다*/
fxA = fxA - floor (fxA);
/* 이때 fit()을 활용하여 쉐입을 뒤집어 버렸다. 이는 나중에 chramp()를 적용하였을때 모션이 진행될때
ramp가 x값으로 봤을때 0에서부터 1까지 나타나게 하기 위함이다.*/
fxA = fit (fxA, 0, 1, 1, 0);
fxA = chramp ("FXA", fxA); // chramp()을 통해 파형의 모양을 형성하였다
// fxA에 dist + 1한 값을 나눠주어 마치 원점으로부터 거리 길이 값이 커질 수록 effect가 약해지는 것처럼 표현
// dist에 1을 더하여 1보다 큰 양수값이 되어 나눗셈이 올바르게 작동될수 있게하여라
// pow()을 이용하여 나누는 값에 제곱을 해주어 더욱 빠르게 줄어들 수 있게하여라
// pow()안에 chf()을 집어넣어 제곱의 지수의 값을 파라미터로 조절할 수 있게함.
fxA /= pow ((dist + 1), chf ("DIM"));
/* 0번 인풋으로 들어온 Geometry를 구성하는 모든 포인트들과 방금 전 저장한 1번 geometry에 Pt값에 해당하는
포인트들의 위치값들 사이의 거리 길이를 구하여 float variable dist에 저장하여라*/
// 이 값을 Float variable cutoff에 또 저장하여라
// effect (물결 모양)가 허용되는 범위를 지정해준다.
float cutoff = dist;
// keep은 effect (물결 모양)을 유지해주는 거리 길이
float keep = chf ("KEEP");
// keep은 effect (물결 모양)을 끝내주는 거리 길이
float end = chf ("END");
// if statement
// 만약 물결 모양의 범위가 유지해 주는 거리길이보다 크고 끝내주는 거리 길이보다 적으면
if (cutoff > keep && cutoff < end) {
// keep과 end수치 사이에 있는 물결 모양의 거리를 1에서 0으로 내려가게끔 하여라
cutoff = fit (cutoff, keep, end, 1, 0);
// 만약 물결 모양의 범위가 유지해주는 거리길이보다 적으면
} else if (cutoff <= keep) {
cutoff = 1; // 물결 모양의 거리를 1로 바꿈
} else { // 물결모양의 범위가 유지해 주는 거리길이와 끝내주는 거리길이보다 모두 크면
cutoff = 0; // 물결 모양의 범위는 0이된다.
}
// 위에 만든 조건문들의 식들을 직관적으로 알아보기 위해 @Cd 컬러값으로 나타내어라
@Cd = set (cutoff, 0, (1-cutoff));
/* * 효과를 택 * */
/* 맨 위에 선언한 float variable fx에 모든 effect 변수와 ramp변수들을 차례대로 추가하여 fx를 순차적으로
업데이트 해주었다. 이때 더하기를 라인마다 쓰는것이 직관적이고 좋다*/
fx += fxA*cutoff;
/* 방금 전 추가해준 모든 ramp안에 지정된 수치값에 따라 반영된 effect들을 포함하는 float variable fx를
@P.y 높이값으로 보여주어라*/
@P.y = @P.y + fx;
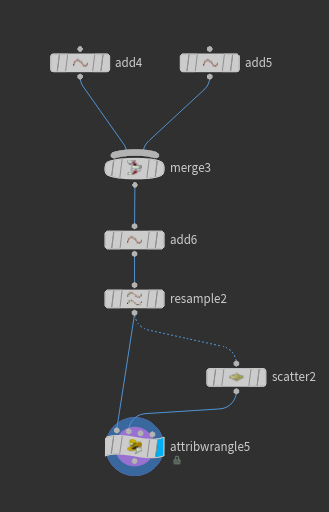
scatter노드를 활용하여 4개의 포인트들을 만들어주고 그 값들을 1번 wrangle node input에 연결하여 nearpoint()을 적용하여 여러개의 Ripple effect가 한 grid에서 나타날 수 있도록 세팅해 주었다.
/* * 변수 생성 & 효과 생성 * */
/* 0번 인풋으로 들어운 geometry의 모든 포인트들로부터 1번 인풋으로 들어온 geometry의
가장 가까운 포인트들의 포인트 넘버를 int variable pt에 저장하여라*/
// 점이 여러개 있을시 pt는 모든 포인트들의 위치에 따라 각기 달라진다
// 가져온 결과 point number 즉 @ptnum임
int pt = nearpoint (1, @P);
// 방금 만들어낸 integer variable pt를 attribute로써 나타내어라
i@pt = pt;
// 여기 float variable fx는 전체적인 effect를 추가한 값임. 모든 효과에 대해 정의를 내려준다.
float fx = 0;
// 여기 float variables은 fx에 추가될 수치들로써 각기 어떠한 효과를 나타낼지 정의를 내려준다.
float fxA = 0;
// 방금 전 1번 인풋으로 연결된 pt에 포인트 넘버가 할당된 포인트들의 위치값을 vector variable hitPos에 저장
vector hitPos = point (1, "P", pt);
/* 0번 인풋으로 들어온 Geometry를 구성하는 모든 포인트들과 방금 전 저장한 1번 geometry에 Pt값에 해당하는
포인트들의 위치값들 사이의 거리 길이를 구하여 float variable dist에 저장하여라*/
float dist = distance (@P, hitPos);
// 여기 float variables은 fx에 추가될 수치들로써 각기 어떠한 효과를 나타낼지 정의를 내려준다.
/* 거리 길이값을 effect fxA에 적용함으로써 1번 인풋 geometry를 구성하는 포인트들을 기점으로 0번
인풋 geometry를 구성하는 모든 점들의 거리길이를 fxA에 저장한다.*/
fxA = dist;
// @Time을 빼주어 움직이는 모션을 취해준다. 빼줌으로써 중심으로부터 바깥으로 빠져나가는 형태의 모션 구축
fxA -= @Time;
/* effect값에 floor()을 적용하여 내림을 취함으로써 높이값으로 나타내었을때 계단같은 형상이 나타나도록 유도
하지만 그 값을 전체 fxA에서 다시 빼서 반복되는 ramp가 나타나는 것처럼 쉐입을 생성하였다*/
fxA = fxA - floor (fxA);
/* 이때 fit()을 활용하여 쉐입을 뒤집어 버렸다. 이는 나중에 chramp()를 적용하였을때 모션이 진행될때
ramp가 x값으로 봤을때 0에서부터 1까지 나타나게 하기 위함이다.*/
fxA = fit (fxA, 0, 1, 1, 0);
fxA = chramp ("FXA", fxA); // chramp()을 통해 파형의 모양을 형성하였다
// fxA에 dist + 1한 값을 나눠주어 마치 원점으로부터 거리 길이 값이 커질 수록 effect가 약해지는 것처럼 표현
// dist에 1을 더하여 1보다 큰 양수값이 되어 나눗셈이 올바르게 작동될수 있게하여라
// pow()을 이용하여 나누는 값에 제곱을 해주어 더욱 빠르게 줄어들 수 있게하여라
// pow()안에 chf()을 집어넣어 제곱의 지수의 값을 파라미터로 조절할 수 있게함.
fxA /= pow ((dist + 1), chf ("DIM"));
/* 0번 인풋으로 들어온 Geometry를 구성하는 모든 포인트들과 방금 전 저장한 1번 geometry에 Pt값에 해당하는
포인트들의 위치값들 사이의 거리 길이를 구하여 float variable dist에 저장하여라*/
// 이 값을 Float variable cutoff에 또 저장하여라
// effect (물결 모양)가 허용되는 범위를 지정해준다.
float cutoff = dist;
// keep은 effect (물결 모양)을 유지해주는 거리 길이
float keep = chf ("KEEP");
// keep은 effect (물결 모양)을 끝내주는 거리 길이
float end = chf ("END");
// if statement
// 만약 물결 모양의 범위가 유지해 주는 거리길이보다 크고 끝내주는 거리 길이보다 적으면
if (cutoff > keep && cutoff < end) {
// keep과 end수치 사이에 있는 물결 모양의 거리를 1에서 0으로 내려가게끔 하여라
cutoff = fit (cutoff, keep, end, 1, 0);
// 만약 물결 모양의 범위가 유지해주는 거리길이보다 적으면
} else if (cutoff <= keep) {
cutoff = 1; // 물결 모양의 거리를 1로 바꿈
} else { // 물결모양의 범위가 유지해 주는 거리길이와 끝내주는 거리길이보다 모두 크면
cutoff = 0; // 물결 모양의 범위는 0이된다.
}
// 위에 만든 조건문들의 식들을 직관적으로 알아보기 위해 @Cd 컬러값으로 나타내어라
@Cd = set (cutoff, 0, (1-cutoff));
/* * 효과를 택 * */
/* 맨 위에 선언한 float variable fx에 모든 effect 변수와 ramp변수들을 차례대로 추가하여 fx를 순차적으로
업데이트 해주었다. 이때 더하기를 라인마다 쓰는것이 직관적이고 좋다*/
fx += fxA*cutoff;
/* 방금 전 추가해준 모든 ramp안에 지정된 수치값에 따라 반영된 effect들을 포함하는 float variable fx를
@P.y 높이값으로 보여주어라*/
@P.y = @P.y + fx;
이해가 안되었던 부분:
- 이번 강의는 솔직히 말해서 어려웠다. 말로 풀어 쓰기 가장 어려웠던 강의였던 것 같다. 마지막에 cutoff와 keep 그리고 end variable을 이용하여 파형의 거리값이 얼마나 진행될지의 관한 조건문들을 해석하는 것이 난관이었던 것 같다. 아마 계속 연구하여 어떻게 작동되는지 알아봐야 할 것 같다.
공부하면서 들었던 생각:
12일차에 관한 내용은 7일차때 배웠던 nearpoint()에 관한 내용이 많았던 것 같다. 그것을 이용한 과정들이 이제 마치 중요하게 작용하여 진도를 나아갈수록 더욱 비중이 커져가는 것을 느꼈다. ripple effect를 만드는데 이렇게 까지 디테일하게 쉐입을 잡아줘야 하구나라는 생각도 많이 들었던 것 같다. 이번 강의는 난이도에 걸맞게 강의를 한번 더 봐야할 것 같은 예정이다. 다음 강의들인 중첩을 계속 다 보고 시간이 남을때 이번 강의를 다시한번 볼 것이다. 이제부터 약간 코드가 어지러워보이기 시작한다. 양도 엄청 늘어났을 뿐더러 코드 한줄 한줄 확실하게끔 이해하려고 하는데 생각보다 머릿속에 2프로가 채워지지 않아 완전히 숙달하지 못한 기분이 든다. 마지막 조건문 부분은 강의를 들을때 알쏭달쏭한 기분이 계속 들어 불안한 느낌이 커졌던 것 같다. 그럼에도 불구하고 이번 강의는 중요하다고 생각하므로 이번주 안에 다시한 번 더 들어야 겠다는 생각이 든다. 그리고 이번 다이어리도 계속 공부하여 내가 이해 못한 부분이 있거나 잘못 해석한 부분이 있으니 수정을 시도해봐야 할 것 같다.
'FX > Houdini_Joy of VEX' 카테고리의 다른 글
| Joy of Vex - Day 12-3: nearpoints, arrays (0) | 2022.07.16 |
|---|---|
| Joy of Vex - Day 12-2: overlapping effect (0) | 2022.07.13 |
| Joy of Vex - Recap of Week 3 (0) | 2022.07.11 |
| Joy of Vex - Day 11: if statements (0) | 2022.07.08 |
| Joy of Vex - Day 10: relpointbbox (1) | 2022.07.07 |