중요했던 부분:
- 간단한 코드방식을 통해 grid상에서 effect값에 radius를 조절하는 방법
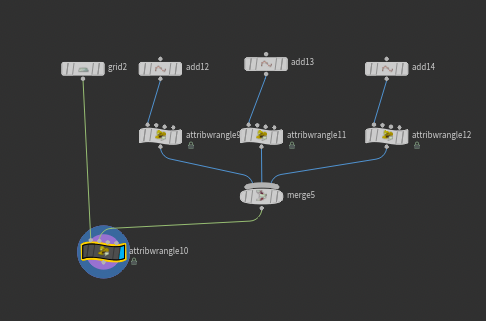
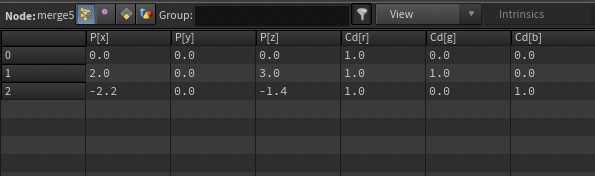
우선 본격적인 강의에 들어가기 앞서 grid와 point를 이용하여 빨간 원을 생성하는 방법을 알아보았고 그의 radius값을 유동적으로 조절할 수 있게끔 코드를 작성하였다. 아래 사진처럼 grid와 point 세 개를 wrangle로 연결한 다음 값을 바꿀때마다 각각의 포인트에 해당하는 effect들을 Grid상에서 나타날 수 있게끔 하였다. 우선 add 노드로 생성된 모든 포인트들을 merge로 묶어서 한눈에 보이게끔 세팅하였고 이는 총 포인트가 세 개 임으로 0/1/2번 포인트로써 한번에 나타나도록 세팅하였다.

@Cd = 0; // 우선 색깔값을 0으로 초기화 검정으로 바꿈
/* 아래 포인트들을 point()으로 불러올때 불러올 포인트 넘버값을 유동적으로 조절할 수 있게 chi()을 사용하여
유저가 파라미터로 포인트 넘버를 조절 할 수 있게끔 세팅하였다*/
int num = chi ("NUM");
/* point()을 이용하여 1번 인풋에 연결된 geometry의 파라미터로 설정된 Num에 해당하는 포인트 넘버를 가진
포인트의 위치값을 불러와 vector variable pos에 저장하여라*/
vector pos = point (1, "P", num);
/* point()을 이용하여 1번 인풋에 연결된 geometry의 파라미터로 설정된 Num에 해당하는 포인트 넘버를 가진
색깔값을 불러와 vector variable color에 저장하여라*/
vector color = point (1, "Cd", num);
/* 포인트 위치로부터 0번 인풋으로 들어온 geometry의 모든 포인트와 방금 전 선언한
1번 인풋으로 들어온 geometry의 num에 해당하는 포인트 넘버를 가진 포인트의 위치값 까지의 거리길이를 구하여
float variable d에 저장하여라*/
float d = distance (@P, pos);
// 유저가 float variable rad를 chf()을 사용하여 파라미터로 지정하여 유동적으로 조절할 수 있게 함
float rad = chf ("RADIUS");
/* 위의 사진에서 설명한 것처럼 포인트로부터 grid를 구성하는 포인트들의 거리가 멀어질수록 오히려 효과는
옅어져야 하기때문에 fit()을 사용하여 거리의 range를 뒤집어 주었다. 그리고 유저가 지정한 RADIUS 파라미터
결과값을 넘으면 더이상 효과가 나타나지 않도록 설정해주기 위해 fit()의 세번째 인풋 (clamp()와 동일한 기능을 담당)
에 rad를 집어넣어주어 효과의 한계 거리를 지정해 주었다*/
d = fit (d, 0, rad, 1, 0);
/* 방금 전 선언한 vector variable color값 즉 포인트의 색깔과 d값을 곱해주어 유저가 설정한 반경안에 포인트로
인한 색깔 문양이 grid에 나타날 수 있도록 설정*/
@Cd = color*d;


- 지난 강의 때 배운 nearpoint()를 활용하여 최대한 이 포인트들의 효과들을 한 grid상에서 중첩시키는 방법
윗 세개의 사진과 같이 이는 num을 파라미터로 조절해야지만 따로따로 효과들을 볼 수 밖에 없었다. 이를 grid상에서 한 번에 보기 위해서는 nearpoint()와 같은 Function을 사용하는 방법도 있었다.
@Cd = 0; // 우선 색깔값을 0으로 초기화 검정으로 바꿈
/* nearpoint()를 활용하여 0번 인풋으로 들어온 Geometry로부터 1번 인풋으로 들어온
geometry를 구성하는 모든 점들중 가장 가까운 점들의 포인트 넘버를 integer variable pt에 저장하여라*/
int pt = nearpoint (1, @P);
/* nearpoint()로 생성된 integer variable pt값을 attribute로 geometry spreadsheet에 디스플레이해라
이는 grid를 구성하는 모든 포인트들이 각기 1번 인풋으로 들어온 Geometry를 구성하는 포인트들중 각기 가장 가까운
포인트들의 포인트 넘버를 찾아 자신들의 @pt 정보에 할당하는 것을 볼 수 있음*/
i@pt = pt;
/* Day 7강의 에서도 배웠듯이
nearpoint()를 사용하면 마치 voronoi texture같은 형태로 변하여 grid상에서 세 개의 포인트들의 위치 상에
따라 구역이 나뉘어지는 것을 관찰할 수 있다.*/
/* point()을 이용하여 0번 인풋에 연결 된 Geometry로부터
1번 인풋에 연결된 geometry중 각기 가장 가까운 포인트들의 포인트 넘버를 가진 포인트의 위치값을 불러와
vector variable pos에 저장하여라*/
vector pos = point (1, "P", pt);
/* point()을 이용하여 0번 인풋에 연결 된 Geometry로부터
1번 인풋에 연결된 geometry중 각기 가장 가까운 포인트들의 포인트 넘버를 가진 색깔값을 불러와
vector variable pos에 저장하여라*/
vector color = point (1, "Cd", pt);
/* 아래 식들은 위에 작성한 코드와 전면 동일함. 거리 길이를 구하여 radius값을 한계로 효과를 주기위해 fit()을
활용하여 거리길이를 조절하고 그 값을 각각 포인트들의 색으로 나타내기 위해 @Cd값에 정해줌*/
float d = distance (@P, pos);
float rad = chf ("RADIUS");
d = fit (d, 0, rad, 1, 0);
@Cd = color*d;
nearpoint()를 활용한 방법은 한 가지 치명적인 단점이 있는데 중첩을 하려고 시도할때 효과들이 overlapping 겹쳐지지 않는다. 마치 voronoi texture처럼 각기 구역을 나뉘어 nearpoint()로 생성된 그 포인트 넘버에 할당되지 않는 grid의 포인트들은 절대로 침범할 수 없는 것처럼 보인다. 쉽게 말하자면 마치 보라색이 할당된 값은 보라색, 빨간색이 할당된 값은 빨간색, 그리고 노란색이 할당된 값은 노란색 이렇게 딱딱 구역이 맞추어져 중첩에 효과가 덜 나게 한다.
- 각각의 1번 wrangle node인풋으로 들어온 geometry의 point에 따른 fx (effect)들을 담당하는 각기 다른 여러 variable 변수들을 생성하여 총 fx에 추가해줘서 중첩을 시켜주는 방법
이는 Day 10때 배운것 처럼 각기 다른 효과들을 할당하는 fx variables 들을 여러개 생성시켜 모든 variable들을 attribute으로 모두 나타내어 grid상에서 모든 효과들을 한눈에 볼 수 있게 하는 방법이다.
/* * 변수 생성 & 효과 생성 * */
@Cd = 0; // @Cd값을 조절하여 색깔값을 0으로 초기화
vector fx = 0; // 모든 효과 effect들을 집어넣기 위한 vector variable fx생성
/* 효과의 반경을 유저가 파라미터로 지정할 수 있도록 chf()로 설정된 값을 float variable rad에 저장*/
float rad = chf ("RADIUS");
/* 아까 위에서 만든 동일한 식들을 0번 포인트에 대해서만 효과를 만들 수 있도록 적용하여 효과들을 생성하기 위한
여러 variable들을 생성. (posA, colA, dA)*/
vector posA = point (1, "P", 0);
vector colA = point (1, "Cd", 0);
float dA = distance (@P, posA);
dA = fit (dA, 0, rad, 1, 0);
/* 아까 위에서 만든 동일한 식들을 1번 포인트에 대해서만 효과를 만들 수 있도록 적용하여 효과들을 생성하기 위한
여러 variable들을 생성. (posB, colB, dB)*/
vector posB = point (1, "P", 1);
vector colB = point (1, "Cd", 1);
float dB = distance (@P, posB);
dB = fit (dB, 0, rad, 1, 0);
/* 아까 위에서 만든 동일한 식들을 2번 포인트에 대해서만 효과를 만들 수 있도록 적용하여 효과들을 생성하기 위한
여러 variable들을 생성. (posC, colC, dC)*/
vector posC = point (1, "P", 2);
vector colC = point (1, "Cd", 2);
float dC = distance (@P, posC);
dC = fit (dC, 0, rad, 1, 0);
/* 방금전 생성한 모든 variable들을 알맞은 fx값들에 저장함. 이때 색깔값과 거리값을 곱한 값을 fx값에 저장하여
반경안에 포인트들의 색깔을 효과로써 나타낼 수 있도록 하여라*/
vector fxA = colA*dA;
vector fxB = colB*dB;
vector fxC = colC*dC;
/* * 효과를 택 * */
/* 맨 위에 선언한 float variable fx에 모든 effect 변수들을 차례대로 추가하여 fx를 순차적으로
업데이트 해주었다. 이때 더하기를 라인마다 쓰는것이 직관적이고 좋다*/
fx += fxA;
fx += fxB;
fx += fxC;
/* * 원본에 저장 * */
/* 방금 전 추가해준 반영된 effect들을 포함하는 float variable fx를
@Cd 색깔값으로 보여주어라*/
@Cd = fx;
하지만 이러한 코드 방식에서도 치명적인 문제가 하나가 있는데 이는 코드에 쓰이는 variable 변수의 양들이 현저하게 많아진다는 것이었다. 이는 나중에 코드를 읽어볼때 직관적인 형태로 알아보지 못하게끔 만드는 등의 문제가 있어 variable의 사용을 줄이는 동시에 중첩에 효과가 온전히 나타나게 할 수 있도록 새로운 방법을 필요로 한다.
- 각각의 fx (effect)들을 담당하는 변수들을 만들어주어 그것들을 총 fx에 추가해줘서 중첩을 시켜주는 방법.
이는 기존에 모든 1번 인풋으로 들어온 geometry를 구성하는 모든 포인트들에게 각기 다른 fx variable들을 생성시켰던것과는 다르게 이번엔 그 fx variable들에게 값을 새롭게 정의해주어 위에서 선언된 값을 무시하고 새로운 값이 저장되는 식으로 바꾸었다.
/* * 변수 생성 & 효과 생성 * */
@Cd = 0; // @Cd값을 조절하여 색깔값을 0으로 초기화
vector fx = 0; // 모든 효과 effect들을 집어넣기 위한 vector variable fx생성
/* 효과의 반경을 유저가 파라미터로 지정할 수 있도록 chf()로 설정된 값을 float variable rad에 저장*/
float rad = chf ("RADIUS");
// 나중에 효과들을 저장할 variable들을 미리 생성함
vector pos = 0;
vector col = 0;
vector d = 0;
/* 이번에는 아까와는 다르게 variable들을 한가지의 종류로만 생성하여 그 variable들의 값들에 또 새로운
값들을 저장시켜 이전 값들은 지워버리고 새로운 값들을 포함하는 식으로 하게끔 세팅하였다*/
/* 아까 위에서 만든 동일한 식들을 0번 포인트에 대해서만 효과를 만들 수 있도록 적용하여 효과들을 생성하기 위한
여러 variable들을 생성.*/
pos = point (1, "P", 0);
col = point (1, "Cd", 0);
d = distance (@P, pos);
d = fit (d, 0, rad, 1, 0);
// 기존에 잇던 값들을 유지한채 새로운 값들을 추가하여 효과들이 누적될 수 있게끔 세팅하였다
fx += col*d;
/* 아까 위에서 만든 동일한 식들을 1번 포인트에 대해서만 효과를 만들 수 있도록 적용하여 효과들을 생성하기 위한
여러 variable들을 생성.*/
pos = point (1, "P", 1);
col = point (1, "Cd", 1);
d = distance (@P, pos);
d = fit (d, 0, rad, 1, 0);
// 기존에 잇던 값들을 유지한채 새로운 값들을 추가하여 효과들이 누적될 수 있게끔 세팅하였다
fx += col*d;
/* 아까 위에서 만든 동일한 식들을 2번 포인트에 대해서만 효과를 만들 수 있도록 적용하여 효과들을 생성하기 위한
여러 variable들을 생성.*/
pos = point (1, "P", 2);
col = point (1, "Cd", 2);
d = distance (@P, pos);
d = fit (d, 0, rad, 1, 0);
// 기존에 잇던 값들을 유지한채 새로운 값들을 추가하여 효과들이 누적될 수 있게끔 세팅하였다
fx += col*d;
/* * 원본에 저장 * */
/* 방금 전 추가해준 모든 반영된 effect들을 포함하는 float variable fx를
@Cd 색깔값으로 보여주어라*/
@Cd = fx;
이번에 구성한 코드 형식에는 매우 중요한 특징이있는데 pos, col, 그리고 d같은 variable들을 해당 포인트에 대해 따로따로 설정해 주지 않고 한번씩만 생성하여 다음 포인트에 대해 효과를 부여할때 곧바로 새로운 값들을 저장시켜 기존의 값들을 지워버리고 새로운 값으로 바뀌게끔 하였다.
int foo = 0;
foo = 2; // int variable foo가 2였는데
foo = 5; // 5로 바뀜마치 이러한 방식으로 지속적으로 variable들을 바꾸어 주었다.
하지만 그러면 효과들은 어떻게 중첩이 되어 나타났을까?
이는 vector variable fx에만 "="이 아닌 "+="와 같은 식을 사용하여 기존에 있던 값들을 유지한체 새로운 값들을 추가하게끔 구성하였다.
그래서 만약 Grid상에서 한 포인트의 위치가 여러 색이 겹쳐진 위치라면
fx = {0.5, 0, 0} + {0, 0.1, 0} + {0, 0, 0} = {0.5, 0.1, 0} 과 같은 식으로 계산이 되어 그에 알맞는 색깔을 띄게 된다.
vector fx = 0;
fx += 5; // 여기서 fx는 0에서 5가 더해져 5의 값을 가지게 되고
fx += 7; // 누적된 5에 7이 또 더해져 12라는 누적된 값을 가지게 된다
- 물결모양에 적용
우선 grid에 물결모양을 생성시키기 위해 물결모양을 생성하는 효과를 수치로써 지정해주어 scene view에서 모션이 나타나도록 하였다.
/* * 변수 생성 * */
//각각에 효과값이 들어갈 변수들을 생성해준다
// 여기 float variable fx는 전체적인 effect를 추가한 값임. 모든 효과에 대해 정의를 내려준다.
float fx = 0;
// 여기 float variables은 fx에 추가될 수치들로써 각기 어떠한 효과를 나타낼지 정의를 내려준다.
float fxA = 0;
// 나중에 값을 지정해줄 변수들을 미리 설정함
vector pos = 0;
float d = 0;
// 유저가 float variable rad를 chf()을 사용하여 파라미터로 지정하여 유동적으로 조절할 수 있게 함
float rad = chf ("RADIUS");
/* 아래 포인트들을 point()으로 불러올때 불러올 포인트 넘버값을 유동적으로 조절할 수 있게 chi()을 사용하여
유저가 파라미터로 포인트 넘버를 조절 할 수 있게끔 세팅하였다*/
int pt = chi ("PT");
/* point()을 이용하여 1번 인풋에 연결된 geometry의 파라미터로 설정된 PT에 해당하는 포인트 넘버를 가진
포인트의 위치값을 불러와 vector variable pos에 저장하여라*/
pos = point (1, "P", pt);
/*1번 인풋으로 들어온 geometry의 num에 해당하는 포인트 넘버를 가진 포인트의 위치값 까지의 거리길이를 구하여
float variable d에 저장하여라*/
d = distance (@P, pos);
/* * 효과 생성 * */
fxA = d; // d의 값에 변화를 주기위해 d의 값을 float variable fxA에 저장
fxA *= chf ("FREQ"); // d의 값을 가진 fxA에 파형이 설정되었을때 freqency를 조절하게끔 설정
// Arithmetic Operation
fxA -= @Time*chf ("SPEED"); // d의 값을 가진 fxA에 파형이 설정되었을때 모션이 작동되고 스피드를 조절하게끔 설정
fxA = sin (fxA); // fxA값에 sin()을 이용하여 sine wave의 형태를 가진 파형을 생성
fxA *= chf ("AMP"); // 이미 만들어진 sine 파형에 높이값을 조절할 수 있게함
// sine wave에서 유저가 설정한 RADIUS수치 이상의 반경 이상 파형이 생성되지 않도록 fit()을 사용하여 구현
fxA *= fit (d, 0, rad, 1, 0);
/* * 효과를 택 * */
// 지금까지 설정한 모든 효과값들을 fx값으로 저장
fx += fxA;
/* * 원본에 저장 * */
/* 방금 전 추가해준 모든 ramp안에 지정된 수치값에 따라 반영된 effect들을 포함하는 float variable fx를
@P.y 높이값으로 보여주어라*/
@P.y += fx;그리고 만든 파형을 우선 nearpoint()를 활용하여 중첩을 시켜보도록 시도하였다. 이는 아까 색깔로써 중첩을 나타낸 것처럼 파형이 서로 만났을때 섞이지 않고 바운더리를 유지한채 각자의 파형을 생성시키는 것처럼 보인다.
/* * 변수 생성 * */
//각각에 효과값이 들어갈 변수들을 생성해준다
// 여기 float variable fx는 전체적인 effect를 추가한 값임. 모든 효과에 대해 정의를 내려준다.
float fx = 0;
// 여기 float variables은 fx에 추가될 수치들로써 각기 어떠한 효과를 나타낼지 정의를 내려준다.
float fxA = 0;
// 나중에 값을 지정해줄 변수들을 미리 설정함
vector pos = 0;
float d = 0;
// 유저가 float variable rad를 chf()을 사용하여 파라미터로 지정하여 유동적으로 조절할 수 있게 함
float rad = chf ("RADIUS");
/* nearpoint()를 활용하여 0번 인풋으로 들어온 Geometry로부터 1번 인풋으로 들어온
geometry를 구성하는 모든 점들중 가장 가까운 점들의 포인트 넘버를 integer variable pt에 저장하여라*/
/*이는 grid를 구성하는 모든 포인트들이 각기 1번 인풋으로 들어온 Geometry를 구성하는 포인트들중 각기 가장 가까운
포인트들의 포인트 넘버를 찾아 자신들의 @pt 정보에 할당하는 것을 볼 수 있음*/
int pt = nearpoint (1, @P);
/* point()을 이용하여 0번 인풋에 연결 된 Geometry로부터
1번 인풋에 연결된 geometry중 각기 가장 가까운 포인트들의 포인트 넘버를 가진 포인트의 위치값을 불러와
vector variable pos에 저장하여라*/
pos = point (1, "P", pt);
/* grid를 구성하는 모든 포인트들의 위치로부터 방금전 선언한 가까운 포인트들의 위치값 까지의 거리길이를
float variable d에 저장*/
d = distance (@P, pos);
/* * 효과 생성 * */
fxA = d; // d의 값에 변화를 주기위해 d의 값을 float variable fxA에 저장
fxA *= chf ("FREQ"); // d의 값을 가진 fxA에 파형이 설정되었을때 freqency를 조절하게끔 설정
// Arithmetic Operation
fxA -= @Time*chf ("SPEED"); // d의 값을 가진 fxA에 파형이 설정되었을때 모션이 작동되고 스피드를 조절하게끔 설정
fxA = sin (fxA); // fxA값에 sin()을 이용하여 sine wave의 형태를 가진 파형을 생성
fxA *= chf ("AMP"); // 이미 만들어진 sine 파형에 높이값을 조절할 수 있게함
// sine wave에서 유저가 설정한 RADIUS수치 이상의 반경 이상 파형이 생성되지 않도록 fit()을 사용하여 구현
fxA *= fit (d, 0, rad, 1, 0);
/* * 효과를 택 * */
// 지금까지 설정한 모든 효과값들을 fx값으로 저장
fx += fxA;
/* * 원본에 저장 * */
/* 방금 전 추가해준 모든 ramp안에 지정된 수치값에 따라 반영된 effect들을 포함하는 float variable fx를
@P.y 높이값으로 보여주어라*/
@P.y += fx;
이를 보완하기 위해 nearpoint()가 아닌 위에 색깔 예시에서 마지막으로 사용한 효과들을 누적시키는 방법을 사용하여 효과적인 파형의 중첩을 구현하였다.
/* * 변수 생성 & 효과 생성 * */
// 여기 float variable FX는 전체적인 effect를 추가한 값임. 모든 효과에 대해 정의를 내려준다.
float FX = 0;
// 여기 float variable fx는 FX에 추가될 수치들로써 각기 어떠한 효과를 나타낼지 정의를 내려준다.
float fx = 0;
// 나중에 값을 지정해줄 변수들을 미리 설정함
vector pos = 0;
float d = 0;
// 유저가 float variable rad를 chf()을 사용하여 파라미터로 지정하여 유동적으로 조절할 수 있게 함
float rad = chf ("RADIUS");
// 이 부분에서는 윗 코드에서 작성한 동일한 효과들의 식들을 작성하였다
// 그대신 point()의 세번째 인풋값을 각기 다르게하여 각기 다른 포인트의 위치에 대해 효과를 생성하게끔 설정하였다
// 이는 계속 변수에 값을 새롭게 정의해주면서 위에서 선언된 값들을 무시하고 새로운 값들을 변수에 저장시켜 바뀌게 했다
/* point()을 이용하여 1번 인풋에 연결된 geometry의 파라미터로 설정된 0번 포인트 넘버를 가진
포인트의 위치값을 불러와 vector variable pos에 저장하여라*/
pos = point (1, "P", 0);
d = distance (@P, pos);
fx = d;
fx *= chf ("FREQ");
// Arithmetic Operation
fx -= @Time*chf ("SPEED");
fx = sin (fx);
fx *= chf ("AMP");
fx *= fit (d, 0, rad, 1, 0);
// 기존에 잇던 값들을 유지한채 새로운 값들을 추가하여 효과들이 누적될 수 있게끔 세팅하였다
FX += fx;
/* point()을 이용하여 1번 인풋에 연결된 geometry의 파라미터로 설정된 1번 포인트 넘버를 가진
포인트의 위치값을 불러와 vector variable pos에 저장하여라*/
pos = point (1, "P", 1);
d = distance (@P, pos);
fx = d;
fx *= chf ("FREQ");
// Arithmetic Operation
fx -= @Time*chf ("SPEED");
fx = sin (fx);
fx *= chf ("AMP");
fx *= fit (d, 0, rad, 1, 0);
// 기존에 잇던 값들을 유지한채 새로운 값들을 추가하여 효과들이 누적될 수 있게끔 세팅하였다
FX += fx;
/* point()을 이용하여 1번 인풋에 연결된 geometry의 파라미터로 설정된 2번 포인트 넘버를 가진
포인트의 위치값을 불러와 vector variable pos에 저장하여라*/
pos = point (1, "P", 2);
d = distance (@P, pos);
fx = d;
fx *= chf ("FREQ");
// Arithmetic Operation
fx -= @Time*chf ("SPEED");
fx = sin (fx);
fx *= chf ("AMP");
fx *= fit (d, 0, rad, 1, 0);
// 기존에 잇던 값들을 유지한채 새로운 값들을 추가하여 효과들이 누적될 수 있게끔 세팅하였다
FX += fx;
/* * 원본에 저장 * */
/* 방금 전 추가해준 모든 ramp안에 지정된 수치값에 따라 반영된 effect들을 포함하는 float variable fx를
@P.y 높이값으로 보여주어라*/
@P.y += FX;
드디어 파형이 겹쳐졌을때 바운더리를 생성하지 않고 자연스럽게 섞여가는 모양의 모션을 완성하였다. 하지만 문제가 있다. 코드에 있는 효과를 생성해주는 식들을 각각의 포인트들의 위치에서 생기게끔 복사 붙여넣기 해서 코드의 양이 너무 길어졌다는 것이다. 이는 여전히 직관적인 형태에서 멀리 떨어져 있는 것을 알 수 있다.
아마 다음 강의에서 배우게 될 array와 for loop 반복문을 통해 이 문제를 해결할 것 같다. 자바를 배웠을때 array와 for loop 모두에 대해 배운적이 있다. 아마 그 방식을 이 코드에 적용하려면 아마 이러한 형태로 될것 이라고 예상한다. 그대신 VEX는 자바와 같은 문법을 채택하지 않으므로 정확히 어떻게 쓰여져 질건지는 확실치 않다. 그래도 아마 다음 강의에 있어 이렇게 가르치실것이라 예상되어 그나마 한시름을 놓을 수 있을 것 같다. (아니면 아예 for loop을 코드가 아닌 노드방식을 사용하여 구성할 지도 모른다...!).
// 총 세 개의 값을 포함하고 있는 array를 만들어 integer array variable pt에 저장
int[]pt = new int [3];
// for loop이 pos의 세번째 인풋의 값이 0에서 2까지 계속 바뀔동안 아래에 있는 효과 식들을 계속 저장해준다
for (int i = 0; i < pt.length; i++) {
pos = point (1, "P", i); // point()의 세번째 값을 i 변수로 설정하여 계속 업데이트 되게끔 함
d = distance (@P, pos);
fx = d;
fx *= chf ("FREQ");
fx -= @Time*chf ("SPEED");
fx = sin (fx);
fx *= chf ("AMP");
fx *= fit (d, 0, rad, 1, 0);
}이해가 안되었던 부분:
- 이상하다. 내용은 점점 더 어려워지고 복잡해가는데 생각보다 마지막에 돌아봤을 때 딱히 이해가 안되는 부분은 없는것 같다. 그치만 코드가 여전히 더욱 복잡해짐에 따라 이해하는데 시간에 꽤 소요가 되고 더욱 갈 수록 직관적으로 쉽게 이해하기 어려워지는 형태가 되는것 같다. 또한 grid와 point들로 wrangle을 연결할 때뿐만이 아닌 조금더 입체적인 geometry들을 wrangle로 연결하였을때 어떠한 쉐입과 모션이 나타날지 예상하는 것에 난관을 느낄것 같다. 이번주 강의에서는 공통적으로 반복적으로 강의없이 작업들을 진행해서 온전히 나만에 것으로 만드는 것이 더욱 중요하게 여겨지는 것같다. 아마 복습일기를 할때 집중적으로 파고들어야 할 것 같다.
공부하면서 들었던 생각:
코드가 이제 점차 길어지고 복잡해지면서 말로 풀어쓰기가 꽤나 난감해지는 상황이 온것같다. 글을 쓰면서도 내가 어떠한 말을 써야할지 감이 잡히지 않는다. 머릿속에는 그래도 개념이 잡혀있는 것이 느껴지는데 막상 말로 코드 한줄 한줄 해석하자니 내가 어떠한 말로써 이것을 설명해야 할지 대략 난감해지는 것 같다. 그래도 드디어 Joy of Vex 코스 초반부터 궁금해왔던 동일한 파형/효과를 어떻게 한 grid안에서 한 번에 보여지게끔 하는 것을 드디어 배운 것 같아 후련하다. nearpoint()를 이용했던 방법은 효과들을 한번에 보이는 것이 가능했지만 효과들 사이사이 바운더리가 보여지는 것이 거슬리게 느끼기도 하였기 때문이다. 이제 완벽하게 효과들을 중첩시키는 방법을 알아 좀더 리얼한 형태의 모션을 추구할 수 있을 것 같다. 근데 그럴수록 모든 포인트의 위치에 대해 효과들을 복사 붙여넣기 하여 쓸대없이 너무 긴 코드를 작성하는 것 같아 더욱 array와 For loop의 강의를 본격적으로 기다리게 만들고 있다. 과연 내가 자바로 배웠던 array와 loop들은 vex와 비교했을때 어떻게 다를지 기대되고 nearpoints()는 과연 일반적인 nearpoint()와는 무슨 차이가 있을지 궁금케 만든다.
'FX > Houdini_Joy of VEX' 카테고리의 다른 글
| Joy of Vex - Day 13: for loops (ties nicely into arrays) (0) | 2022.07.18 |
|---|---|
| Joy of Vex - Day 12-3: nearpoints, arrays (0) | 2022.07.16 |
| Joy of Vex - Day 12-1: ripple effect (0) | 2022.07.13 |
| Joy of Vex - Recap of Week 3 (0) | 2022.07.11 |
| Joy of Vex - Day 11: if statements (0) | 2022.07.08 |