중요했던 부분:
- nearpoint(): Nearpoint Function
지난 시간에 배웠듯이 nearpoint()를 사용한채 grid상에서 파형을 여러개 생성시킬때는 구획이 나눠지는 단점이 있다. 그러므로 중첩을 표현하기 위해 모든 포인트의 정보를 불러와 그리고 효과에 대한 식의 각각 포인트를 넣어주면 거기서 구한 fxA, fxB, fxC와 같은 효과를 생성해 주는 변수들을 모두 누적해 줌으로써 중첩의 효과를 만들어 줄 수 있다. 하지만 이렇게 만들어 주었을때 코드가 굉장히 길어지는 단점을 초래한다.
- nearpoints(): Nearpoints Function
nearpoints()는 가장 가까운 포인트의 위치값을 하나가 아닌 여러개를 찾아준다. 만약 세개의 점이 있다고 했을때 첫번째로 가까운점, 두번째로 가까운점, 그리고 세번쨰로 가까운 점 모두를 찾아주는 function이다.
이는 이러한 형식과 같이 쓰이며:
nearpoints (어디에서 reference를 받을지, 대조하려는 정보, 반경, 찾으려는 포인트의 갯수)
찾으려는 포인트의 갯수는 딱히 정하고 싶지 않으면 설정하지 않아도 된다.
이 값들은 여러개의 수치들을 포함하고 있으므로 array로 생성된 변수안에서만 모두 저장될 수 있다.
단일한 정보: float 2.4, int 2, string TWA
세개의 정보: vector {2, 4, 8}, vector {2.5, 1.2, 0.6} - 이로 보았을때 vector은 세개의 정보를 담아둘 수 있는 고정적 형태의 컨테이너라는 것을 알 수 있다. 그렇다면 세개 이하 혹은 세개 이상의 수치들을 하나의 변수안에서만 저장시키려면? 혹은 변수 안에 수치가 아예 없을 경우 어떻게 선언을 해주어야 할까?
- Array
정보를 담아둘 수 있는 가장 유동적인 형태의 컨테이너. 정보의 갯수에 대한 제한이 없는것이 가장 큰 특징임으로서 정보가 아예 없을 수도 혹은 어마어마하게 많을수도 있다. Array는 정보를 담아주는 녀석으로써 정보의 양이 그때그때 바뀌고 심지어 정보가 없기도 한다. 이는 variable 뒤에 "[]"이라 설정하면서 생성해주거나 attribute 앞에 "[]"이라 설정해주면서 생성한다.
// nearpoint()를 이용하였을때
/* 모든 포인트의 포지션 정보에 대해서 레퍼런스가 되고있는 점들 중 누가 가장 가까운지 찾아주어라*/
int pt = nearpoint (1, @P);
i@pt = pt;
/* 0번 인풋에 연결된 geometry에서의 각각의 점부터 1번 인풋에 연결된 geometry를 구성하는 점들중 제일 가까운
점들을 반경 4안에서 찾아서 integer variable pts에 array로써 모두 저장하여라*/
int pts[] = nearpoints (1, @P, 4);
i[]@pts = nearpoints (1, @P, 4); // 혹은 윗 수치 설정을 attribute로써 저장할때
/* 반경 4 안에서 가까운 순서대로 다섯개의 포인트들을 찾아내 주세요*/
int pts[]= nearpoints (1, @P, 4, 5);이 이미지에서 반경이 3인 grid상에서 가운데 점을 기준으로 하였을때 nearpoints()를 사용하여 가장 가까운 점들을 순서대로 모두 찾으려고 할때...

// 이런식으로 식을 설정해주면
/* 0번 인풋에 연결된 geometry에서의 각각의 점부터 1번 인풋에 연결된 geometry를 구성하는 점들중 제일 가까운
네 점들을 반경 4안에서 찾아서 integer variable pts에 array로써 모두 저장하여라*/
int pts[] = nearpoints (1, @P, 4, 4);결과값으로 이렇게 나타날 것 이다: [1, 4, 2, 3]
이렇게 나타난 결과값에서 하나의 수치만 불러오고 싶을때는 아래와 같은 방식으로 가능하다.
// vector을 사용했을땐 어떻게 했었을까?
// x/y/z 이렇게 vector variable 안에 있는 값들을 세부적으로 나누어 불러오는 방법이 있었다.
vector A = {2, 4, 7};
float k = A.y; // vector variable A에서 y값만 불러와 Float variable k에 저장하여라
// 이는 이렇게도 가능하였은데
/* 이는 geometry spreadsheet에서 우리가 직접 @attribute를 만들어 수치를 보고싶을때 볼수 있는 형태이다.
eg) twa[0], twa[1], twa[2] */
v@twa = {2, 7, 3}; // 2/7/3 이라는 vector 값을 가진 twa라는 변수가 있었을때
f@firstTwa = @twa[0]; // 위에서 첫번째 정보인 2를 불러와 float attribute firstTwa에 저장이 가능하였다
// 혹은
/* array안에서 불러올 수치의 순서값을 유저가 파라미터로써 조절할 수 있게끔 chi()를 사용하고 그 값을 integer variable
num에 넣는다*/
int num = chi ("NUM");
/* 2, 7, 3이라는 값들을 가진 vector 값을 vector attribute twa에 저장*/
v@twa = {2, 7, 3};
/* @twa라는 vector attribute값에서 num에 해당하는 순서값을 가진 정보를 가져와 float attribute k에 저장
만약 이와같이 수치를 불러오려고 했을시 불러오려는 값이 array안에 없으면 이는 저장할때 값을 0으로 default설정한다.*/
f@k = @twa[num];// Array를 사용할때도 이와 동일하게 작동된다
/* array안에서 불러올 수치의 순서값을 유저가 파라미터로써 조절할 수 있게끔 chi()를 사용하고 그 값을 integer variable
num에 넣는다*/
int num = chi ("NUM");
float twa[] = {1, 2, 3, 4}; // float variable twa값이 1, 2, 3, 4일때
f[]@twa = twa; // [1, 2, 3, 4]값을 가진 twa변수값을 float attribute twa로 표현하여라
/* @twa라는 float attribute값에서 num에 해당하는 순서값을 가진 정보를 가져와 float attribute k에 저장
만약 이와같이 수치를 불러오려고 했을시 불러오려는 값이 array안에 없으면 이는 저장할때 값을 0으로 default설정한다.*/
f@k = @twa[num];/* array안에서 불러올 수치의 순서값을 유저가 파라미터로써 조절할 수 있게끔 chi()를 사용하고 그 값을 integer variable
num에 넣는다*/
int num = chi ("NUM");
// vector array variable twa가 위와 같이 vector값을 세개를 포함하고 있을때
vector twa[] = {{1, 2, 3}, {2, 3, 4}, {4, 5, 6}};
v[]@twa = twa; // 모든 vector값들을 vector array attribute twa로 나타내어라
/* @twa라는 vector attribute값에서 num에 해당하는 순서값을 가진 정보를 가져와 vector attribute k에 저장
만약 이와같이 수치를 불러오려고 했을시 불러오려는 값이 array안에 없으면 이는 저장할때 값을 0으로 default설정한다.*/
v@k = @twa[num];그렇지만 array안에 꼭 수치가 직접들어가지 않고 variable 변수들이 대신 들어갈 때가 있다. 이는 {}같은 방식이 아닌 function을 통해 값을 설정해 주어야 하는데 vector값으로 설정할때는 set()을 이용하였다. 하지만 이번에는 array()를 사용하여 설정해야 올바르게 작동된다.
float a = 5;
float b = 4;
float c = 2;
float d = 2;
/* 아까 명시했듯이 이와 같은 코드 방식은 성립되지 않는다. array안에 variable들을 집어넣고 싶으면 별도의
Function을 필요로 한다*/
f[]@twa = {a, b, c, d};
// 올바른 형태
f[]@twa = array (a, b, c, d);
// @twa값의 두번째 값을 불러와 float attribute k 에 저장하여라
f@k = @twa[1];vector a = {1, 2, 3};
vector b = {4, 5, 6};
vector c = set (@ptnum, @Time, @Frame);
/* 방금전 선언한 모든 vector 값의 variable들을 담아 twa라는 vector array attribute에 저장*/
v[]@twa = array (a, b, c);
// 위에서 선언한 array에서 두번째 vector값만 불러와 vector attribute k에 저장하여라
v@k = @twa[1];- two-dimensional array
이는 array안에 또 다른 array혹은 vector값이 있을때의 상태로써 위의 코드에서 v@k로 가져온 값이 {4, 5, 6}일때 이 vector값에서 한가지의 float수치를 또 가져올 수 있게 할 수 있다.
// 위에서 선언한 array에서 두번째 vector값들중 첫번째 float 수치를 불러와 float attribute k에 저장하여라
f@k = @twa[1][0];이로인해 위에서 선언한 array에서 f@k에 오직 4라는 수치만 저장시킬 수 있다.
- len(): Length Function
len()은 array의 길이값을 구하여 줄 수 있는 function이다. array가 [0, 1, 2, 3, 4]라면 길이값은 5가되고, [2, 3, 4]라면 길이값은 3이된다. 즉 array안에 들어있는 정보들의 숫자가 len()으로 계산되는 결과값이다.
/* 0번 인풋으로 들어온 geometry로부터 1번 인풋으로 들어온 geometry를 구성하는 점들까지의 가장 가까운 점들을
반경 4안에서 찾아 int array attribute pts에 저장시켜라*/
i[]@pts = nearpoints (1, @P, 4);
// array의 길이 값을 각각 구해 int attribute count로 나타내어라
i@count = len (@pts);
nearpoint()와 nearpoints()를 각각 비교하였을때
/* 0번 인풋 geometry로부터 1번 인풋 geometry를 구성하는 점들중 가장 가까운 점들의 포인트 넘버를 찾아서
int variable pt에 저장하여라*/
int pt = nearpoint (1, @P);
/* 1번 인풋 Geometry에서 pt에 해당하는 포인트 넘버를 가진 포인트들의 포인트 위치값들을 0번 geometry의 모든
포인트에 대하여 vector variable pos로 저장하여라*/
vector pos = point (1, "P", pt);
/* 1번 인풋 Geometry에서 pt에 해당하는 포인트 넘버를 가진 포인트들의 색깔값들을 0번 geometry의 모든
포인트에 대하여 vector variable pos로 저장하여라*/
vector pos = point (1, "Cd", pt);
// 1번 인풋 geometry의 포지션의 위치와 1번 인풋 geometry 모든점까지의 거리를 구하라
float d = distance (@P, pos);
/* 방금 구한 distance값을 radius로써 유저가 파라미터로 조절 할수 있게 하고 전체적인 거리 길이는
1에서 0으로 뒤집어 안쪽으로 갈수록 효과값이 높고 가장자리로 갈수록 더욱 떨어지게끔 만들어라*/
d = fit (d, 0, ch ("RADIUS"), 1, 0);
/* 방금전에 선언한 1번 인풋 geometry를 구성하는 point들의 컬러값과 거리값을 곱하여 거리 길이에 따라
컬러가 그만큼의 범위에서 형성될 수 있도록 세팅하여라*/
@Cd = col*d;
/* 0번 인풋 geometry로부터 1번 인풋 geometry를 구성하는 점들중 가장 가까운 점들의 포인트 넘버들을 반경 40안에서
찾아서 int variable pt에 저장하여라*/
int pts[] = nearpoints (1, @P, 40);
i[]@pts = pts; // 찾은 값들을 int attribute pts으로 array로써 볼수 있게끔 나타내어라
// 방금전 생성한 array에서 첫번째 정보만 불러와 int variable pt에 저장하여라
int pt = pts[0];
i@pt = pt; // variable pt를 i@pt로 저장하여 geometry spreadsheet에 디스플레이
// 효과의 반경을 직접 유저가 파라미터로 조절 할 수 있게끔 float variable radius값을 chf()으로 설정
float radius = chf ("RADIUS");
/* 1번 인풋 Geometry에서 pt에 해당하는 포인트 넘버를 가진 포인트들의 포인트 위치값들을 0번 geometry의 모든
포인트에 대하여 vector variable pos로 저장하여라*/
vector pos = point (1, "P", pt);
/* 1번 인풋 Geometry에서 pt에 해당하는 포인트 넘버를 가진 포인트들의 색깔값들을 0번 geometry의 모든
포인트에 대하여 vector variable pos로 저장하여라*/
vector pos = point (1, "Cd", pt);
// 1번 인풋 geometry의 포지션의 위치와 1번 인풋 geometry 모든점까지의 거리를 구하라
float d = distance (@P, pos);
/* 방금 구한 distance값을 radius로써 유저가 파라미터로 조절 할수 있게 하고 전체적인 거리 길이는
1에서 0으로 뒤집어 안쪽으로 갈수록 효과값이 높고 가장자리로 갈수록 더욱 떨어지게끔 만들어라*/
d = fit (d, 0, ch ("RADIUS"), 1, 0);
/* 방금전에 선언한 1번 인풋 geometry를 구성하는 point들의 컬러값과 거리값을 곱하여 거리 길이에 따라
컬러가 그만큼의 범위에서 형성될 수 있도록 세팅하여라*/
@Cd = col*d;이렇게 된다면 array에서 구한 값들중 가장 가까운 거리 [0] 의 포인트위치를 가진 포인트 넘버를 중심으로 효과가 계산되기 때문에 위의 이미지와 같은 똑같은 형식의 쉐입이 나타난다.

그러므로 두번째로 가까운 포인트들을 중심으로 하여 효과를 만들어주려면 [0]가 아닌 [1]으로 설정하여 코드를 작성해야 한다. 이는 중첩이 한번 일어나고 나타나는 효과값을 나타내줌으로써 더욱 적은 범위의 쪼개짐을 나타내는 것을 알 수 있다.
/* 0번 인풋 geometry로부터 1번 인풋 geometry를 구성하는 점들중 가장 가까운 점들의 포인트 넘버들을 반경 40안에서
찾아서 int variable pt에 저장하여라*/
int pts[] = nearpoints (1, @P, 40);
i[]@pts = pts; // 찾은 값들을 int attribute pts으로 array로써 볼수 있게끔 나타내어라
// 방금전 생성한 array에서 두번째 정보 (두번째로 가까운 점들)만 불러와 int variable pt에 저장하여라
int pt = pts[1];
i@pt = pt; // variable pt를 i@pt로 저장하여 geometry spreadsheet에 디스플레이
// 효과의 반경을 직접 유저가 파라미터로 조절 할 수 있게끔 float variable radius값을 chf()으로 설정
float radius = chf ("RADIUS");
/* 1번 인풋 Geometry에서 pt에 해당하는 포인트 넘버를 가진 포인트들의 포인트 위치값들을 0번 geometry의 모든
포인트에 대하여 vector variable pos로 저장하여라*/
vector pos = point (1, "P", pt);
/* 1번 인풋 Geometry에서 pt에 해당하는 포인트 넘버를 가진 포인트들의 색깔값들을 0번 geometry의 모든
포인트에 대하여 vector variable pos로 저장하여라*/
vector pos = point (1, "Cd", pt);
// 1번 인풋 geometry의 포지션의 위치와 1번 인풋 geometry 모든점까지의 거리를 구하라
float d = distance (@P, pos);
/* 방금 구한 distance값을 radius로써 유저가 파라미터로 조절 할수 있게 하고 전체적인 거리 길이는
1에서 0으로 뒤집어 안쪽으로 갈수록 효과값이 높고 가장자리로 갈수록 더욱 떨어지게끔 만들어라*/
d = fit (d, 0, ch ("RADIUS"), 1, 0);
/* 방금전에 선언한 1번 인풋 geometry를 구성하는 point들의 컬러값과 거리값을 곱하여 거리 길이에 따라
컬러가 그만큼의 범위에서 형성될 수 있도록 세팅하여라*/
@Cd = col*d;
이러한 방식을 사용하여 array에서 몇번째 수치를 불러오느냐에 따라 효과의 중첩이 얼마나 많이 될지 선택해 줄 수 있다.
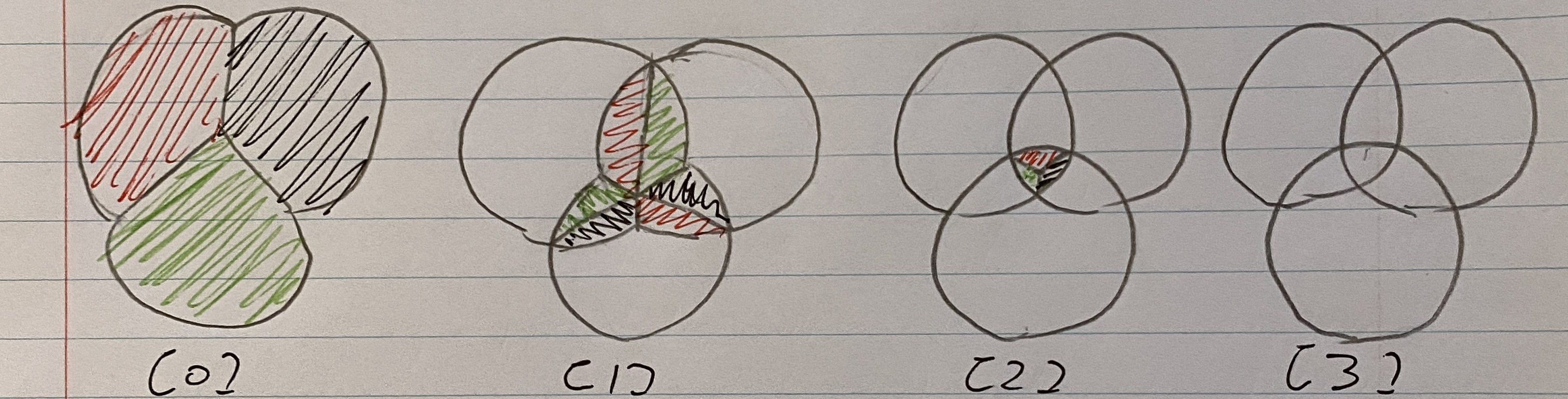
즉 [0]는 중첩이 되지않음
[1]은 한번 중첩된 결과
[2]는 두번 중첩된 결과
[3]은 세번 중첩된 결과로써 알 수 있다.
그러므로 지난 번에 만든 방식으로 fx를 누적시킴으로써 만들었던 중첩은: 각각의 포인트에 대해서 효과를 만들어 주고 그 효과를 누적해줌으로써 결과를 만들었다면... 핵심은 변수 설정을 먼저 해줌으로써 다음에 값들을 다시 복사 붙여넣기 하였을때 type casting 또 안하고도 가능하게 만들수 있다.
이번강의를 통해 만든 방식은: nearpoints()를 이용해서 가장 가까운 녀석에 대해서 색깔 표현을 해주고 중첩 한번/두번 이와 같은 방식으로 포인트의 갯수만큼 중첩의 대한 대비를 한것 이다. 그래서 색깔이 더해지는 효과를 만들어 주었다.
이 두 방식을 전부 적용하여 아래와 같이 중첩을 성공적으로 완성시킬 수 있다.
/* * 변수 설정 * */
vector pos = 0;
vector col = 0;
int pts[];
int pt;
float d = 0;
float radius = chf ("RADIUS");
/* 0번 geometry로부터 1번 geometry를 구성하는 점들중 반경 40안에서 가장 가까운 것들의 포인트 넘버들을 찾아
int array variable pts에 저장하여라*/
pts = nearpoints (1, @P, 40);
@Cd = 0; // @Cd 컬러값을 0으로 초기화
/* * 효과 생성 & 원본에 저장 * */
/* 이 효과들을 전부 array안 각각의 포인트에 대하여 나온 값들을 @Cd값안에 누적시켜 중첩이 되게 하는 방식을 하였다*/
///
pt = pts[0]; // pts array에 있는 값들중 첫번째 값만 pt에 저장
// 1번 인풋 geometry에서 pt에 해당하는 포인트 넘버를 가진 포인트 위치값을 가져와 pos에 저장
pos = point (1, "P", pt);
// 1번 인풋 geometry에서 pt에 해당하는 포인트 넘버를 가진 색깔값을 가져와 pos에 저장
col = point (1, "Cd", pt);
// 방금 선언한 각각의 pos값과 grid상의 모든 포인트 위치사이의 거리길이값을 d에 저장
d = distance (@P, pos);
// fit()을 통해 안쪽으로 갈수록 효과값이 커지고 멀어질수록 떨어지게끔 조정
d = fit (d, 0, radius, 1, 0);
@Cd += col*d; // 이 값들을 색깔로써 보여주게 함
/* 이 다른 포인트들을 중심으로 계속 반복하여 @Cd값에 누적시켜 중첩되는 효과를 만든다*/
///
pt = pts[1];
pos = point (1, "P", pt);
col = point (1, "Cd", pt);
d = distance (@P, pos);
d = fit (d, 0, radius, 1, 0);
@Cd += col*d;
///
pt = pts[2];
pos = point (1, "P", pt);
col = point (1, "Cd", pt);
d = distance (@P, pos);
d = fit (d, 0, radius, 1, 0);
@Cd += col*d;
///
pt = pts[3];
pos = point (1, "P", pt);
col = point (1, "Cd", pt);
d = distance (@P, pos);
d = fit (d, 0, radius, 1, 0);
@Cd += col*d;
///
pt = pts[4];
pos = point (1, "P", pt);
col = point (1, "Cd", pt);
d = distance (@P, pos);
d = fit (d, 0, radius, 1, 0);
@Cd += col*d;
///
pt = pts[5];
pos = point (1, "P", pt);
col = point (1, "Cd", pt);
d = distance (@P, pos);
d = fit (d, 0, radius, 1, 0);
@Cd += col*d;
///
pt = pts[6];
pos = point (1, "P", pt);
col = point (1, "Cd", pt);
d = distance (@P, pos);
d = fit (d, 0, radius, 1, 0);
@Cd += col*d;
이와 같은 방식을 지난 시간에 만들었던 물결모양에 적용한다면 이와 같이 작성할 수 있다.
/* * 변수 설정 * */
int pt;
vector pos = 0;
float d = 0;
float w = 0;
float radius = chf ("RADIUS");
float r = chf ("R");
int num = chi ("NUM");
/* 0번 geometry로부터 1번 geometry를 구성하는 점들중 유저가 선택한 반경안에서 가장 가까운 것들의 포인트 넘버들을 찾아
int array variable pts에 저장하여라*/
pts = nearpoints (1, @P, radius, num);
pt = pts[0]; // pts array에 있는 값들중 첫번째 값만 pt에 저장
// 1번 인풋 geometry에서 pt에 해당하는 포인트 넘버를 가진 포인트 위치값을 가져와 pos에 저장
pos = point (1, "P", pt);
// 방금 선언한 각각의 pos값과 grid상의 모든 포인트 위치사이의 거리길이값을 d에 저장
d = distance (@P, pos);
w = d*ch("FREQ"); // 효과에 freqency를 조절하여 파형의 촘촘함을 설정
w -= @Time*ch ("SPEED"); // 효과의 스피드를 설정
w = sin (w); // 파형이 sin()으로 sine wave로써 나타나게끔 설정
w *= chf ("AMP"); // 파형의 높이값을 설정
w *= fit (d, 0, r, 1, 0); // 포인트로부터 파형이 멀어질수록 효과가 덜나도록 설정
@P.y += w; // 이 모든 효과들을 높이값으로 설정
/* 이 다른 포인트들을 중심으로 계속 반복하여 @P.y값에 누적시켜 중첩되는 효과를 만든다*/
pt = pts[1];
pos = point (1, "P", pt);
d = distance (@P, pos);
w = d*ch("FREQ");
w -= @Time*ch ("SPEED");
w = sin (w);
w *= chf ("AMP");
w *= fit (d, 0, r, 1, 0);
@P.y += w;
pt = pts[2];
pos = point (1, "P", pt);
d = distance (@P, pos);
w = d*ch("FREQ");
w -= @Time*ch ("SPEED");
w = sin (w);
w *= chf ("AMP");
w *= fit (d, 0, r, 1, 0);
@P.y += w;
Exercises:
1. Make this extend beyond to more scatter points by manually copying and pasting
scatter노드로 만들어진 포인트들의 갯수 7개를 넘어 중첩되는 횟수를 10번까지 늘려보았다. 나는 중첩이 정말정말정말 자연스럽게 스무스하게 이어지는 그런 쉐입을 기대했다. 하지만 시도해보았더니 아래와 같은 효과가 나타났다.
2. Make the waves include and mix colour
각각의 효과에 색깔을 섞어 주었더니 아래와 같은 효과가 나타난 것을 알 수 있었다.
3. Do different speeds and amplitudes for each wave hit (hint, you'll need to add a random amount to w somewhere, driven from pt)
각각의 amp와 speed에 chf()을 활용하여 각각 다르게 수치를 설정하게끔 만들어 코드를 작성하였다.
int pts[];
int pt;
vector pos = 0;
float d = 0;
float w = 0;
float radius = chf ("RADIUS");
float r = chf ("R");
int num = chi ("NUM");
pts = nearpoints (1, @P, radius, num);
pt = pts[0];
pos = point (1, "P", pt);
d = distance (@P, pos);
w = d*ch("FREQ");
w -= @Time*ch ("SPEED1");
w = sin (w);
w *= chf ("AMP1");
w *= fit (d, 0, r, 1, 0);
@P.y += w;
pt = pts[1];
pos = point (1, "P", pt);
d = distance (@P, pos);
w = d*ch("FREQ");
w -= @Time*ch ("SPEED2");
w = sin (w);
w *= chf ("AMP2");
w *= fit (d, 0, r, 1, 0);
@P.y += w;
pt = pts[2];
pos = point (1, "P", pt);
d = distance (@P, pos);
w = d*ch("FREQ");
w -= @Time*ch ("SPEED3");
w = sin (w);
w *= chf ("AMP3");
w *= fit (d, 0, r, 1, 0);
@P.y += w;
이해가 안되었던 부분:
- 1번 exercise에서 scatter 노드로 만들어진 포인트의 갯수를 넘어서 중첩되는 횟수를 계속 늘렸을때 하나의 포인트에서 생성된 높이값이 다른 포인트들에 비해 혼자만 커지는 것을 알 수 있었다. 도대체 왜 그런 효과가 나타나는지 알 수 가 없었다. 왜 하나의 포인트에서 값이 값자기 커지고 나머지들은 그대로이고 모두 동등한지 머릿속이 햇갈려지기 시작하였다. 아마 복습일기때 다시 한번 재 검토해보아야할 내용인 것같아 여기에다 써본다.
공부하면서 들었던 생각:
드디어 12일차를 모두 끝냈다... 12일차 솔직히 강의를 3번이나 나누어서 배운내용인만큼 많이 어렵기도 하고 햇갈리기도 하였다. 무엇보다 지난 강의에서 이만큼의 코드의 양을 길게 써본적이 없어 공부하면서 많이 애먹은것같다. 그래도 이제 확실히 array와 nearpoints()의 개념에 대해 확실이 안 만큼 vex로 만들어 볼 수 있는 범위가 많이 확장된것 같아 기분이 좋다. 이번주는 12일차에 대한 12일차를 위한 12일차에 모든 것에 관한 것 같다. 제발 13일차 내용은 이번보다 조금 수월하게 진행됬으면 좋겠다... ㅋㅋ 그래도 12일차를 세번에 나누어 꼼꼼히 배우니 중첩에 관한것은 왠만에서는 이제 확실히 알것같은 기분이 든다. 아마 joy of vex에 있어서 7일차와 12일차가 고비라 들었는데 이제 나머지 남은 코스들은 얼마나 어려울지 기대가 된다.
'FX > Houdini_Joy of VEX' 카테고리의 다른 글
| Joy of Vex - Recap of Week 4 (0) | 2022.07.18 |
|---|---|
| Joy of Vex - Day 13: for loops (ties nicely into arrays) (0) | 2022.07.18 |
| Joy of Vex - Day 12-2: overlapping effect (0) | 2022.07.13 |
| Joy of Vex - Day 12-1: ripple effect (0) | 2022.07.13 |
| Joy of Vex - Recap of Week 3 (0) | 2022.07.11 |