중요했던 부분:
- length(): Length Function
원점 (0, 0, 0) 으로부터, 지정된 인풋의 위치까지의 거리 길이를 구하는 function.
eg) float d = length (@P); // 원점으로부터 포인트 위치까지의 거리 길이를 float variable d에 store 하여라.
// (Formal) 모든 포지션값에 대한 위치 정보를 원점으로 부터의 길이로 측정하십시오. 그리고 그 값은 각각의 포인트에 d 라는 변수로 저장하십시오.
만약 위에서 선언한 float variable d를 sine function과 함께 @Cd (Colour attribute)으로 지정한다면 마치 색깔이 원의 중심으로 부터 퍼져 나가는 파동의 쉐입을 형성한다.
eg) @Cd = sin (d); // 웨이브를 형성함
d = d*chf ("SCALE"); // d는 앞으로 ch()을 곱한 값이 될 것 이다.
위에 코드와 같이 선언한 variable이나 attribute 자체들을 직접 계산하려면 eg) d *= chf ("SCALE"); 과 같이 줄여 쓸 수 있다.
*Day 1 때부터 알았던 상기시키면 좋을 것: 1보다 높은 값이 sin()이나 cos()안에 들어있는 constant나 variable에게 곱해지면 파장은 좁아진다. 반대로 나누면 파장은 넓어진다.
eg) @P.y = sin (d*102); // 파장이 엄청나게 좁아저 촘촘한 웨이브 쉐입을 띄움.
eg) @Cd = cos (23/34); // 파장이 넓어져 상대적으로 원만한 웨이브 쉐입을 띄움.
- Advanced Calculation
eg) @Cd = (sin (d) + 1)*0.5; // -1 부터 1 사이의 range를 0 부터 2 사이의 range로 조정하여 색을 더욱 밝게 만듦. 그리고 밝게 만든 색생을 반으로 나누어 (*0.5는 /2와 같음) 0 부터 1사이의 간격의 밝기로 조정함. 이 식은 나중에 배우게 될 Fit Function과 관계가 밀접함.
- distance(): Distance Function
두 개의 input사이의 거리를 측정하는 function.
*Run Over가 Points로 지정되었을 때*
eg) float dist = distance (@P, {1, 0, 3}); // 모든 포인트에 대한 @P (포인트의 위치)와 vector (1, 0, 3)의 위치 사이에 거리를 측정하여라. 그리고 그 거리 길이들을 float variable dist에 store 하여라.
dist = dist*chf ("SCALE"); // variable dist의 값을 channel function을 활용하여 parameter로서 조정 가능케함.
@Cd = (sin (dist) + 1)*0.5; // sine function을 활용하여 vector (1, 0, 3)의 위치에서 뿜어져 나오는 파동을 형성하고 뒤에 따라오는 상수들의 계산들을 통해 전반적인 색상을 조정함. 아까도 언급했듯이 이것은 fit function으로 더욱 알아보기 쉽게 조정 가능.
- ch()의 응용
chi/chf/chv와 같이 각각의 variable들이나 attribute들의 cast에 맞는 parameter들을 생성하기 위한 function으로써 작동 할 수 있다.
eg) float foo = chf ("SCALE");
eg) v@idk = chv ("adjustAnything");
eg) vector center = chv ("CENTER");
- 파형의 모양을 띄는 그리드를 형성하기 위한 VEX code
eg)
vector pos = @P*chv("FANCYSTYLE"); // 모든 포인트들에 대하여 포인트의 위치를 곱하여 위치를 조정하여라. 예를 들어 (-1, 0, 0)에 위치한 포인트는 1보다 높은 수를 곱하면 더욱 더 큰 마이너스 값을 형성. 반대로 (2, 0, 0)에 위치한 포인트는 1보다 높은 수를 곱하면 더욱 더 큰 플러스 값을 형성. 그러므로 벡터값을 어떠한 수로 곱하였을때 웨이브가 각기 x/y/z 방향으로 늘어나거나 쪼그라들은 웨이브의 형상을 구현할 수 있음. 그리고 그 값들은 vector variable pos에 store됨.
vector center = chv ("CENTER"); // origin 위치 조정.
v@pos = pos; // vector variable pos를 attribute pos에 store 한다. 그러므로 geometry spreadsheet 에 pos를 display할 수 있다.
float d = distance (pos, center); // vector variable pos (포인트들의 위치)와 유저가 지정한 vector variable center (원점)의 거리의 길이를 측정하여라.
d = d*chf ("SCALE"); // d는 앞으로 ch("SCALE")을 곱한 값이 될 것 이다. 파장의 거리 길이를 조정 할 수 있다.
@Cd = (sin (d) + 1)*0.5; // 파장의 거리 길이를 sine function에 적용하여 웨이브의 형태를 구성하는 쉐입을 형성. 그리고 뒤에 따라오는 상수들의 계산을 통해 색상들을 조정 (정확히는 sine 그래프의 위치와 높이를 설정). 그리고 이 모든 것을 @Cd로 표현하여 색상이 반복되는 패턴을 만든다.
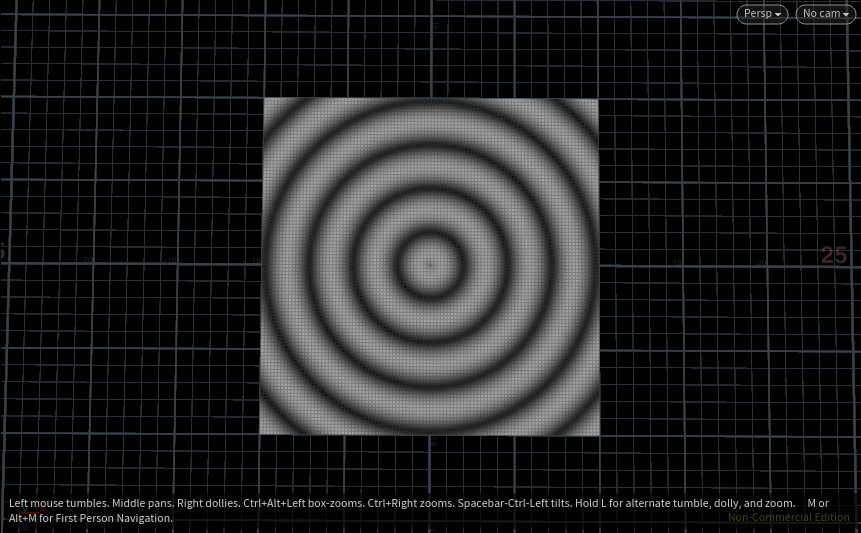
- fit(): Fit Function & Clamp(): Clamp Function
clamp()는 clamp (input, min, max);로 구성되어 있으며 min과 max의 수치 조절을 통해 range에 포함되지 않는 웨이브들을 없애버린다.
fit()은 fit (input, input_min, input_max, output_min, output_max);로 구성되어 있으며 function안에 들어가는 앞에 세개의 값들은 clamp()와 완전히 동일 하며 output_min과 output_max를 통해 웨이브의 모양은 그대로지만 높이값 (range)을 조절할 수 있다. (확대와 축소 기능).
*input의 값들과 output의 값들이 동일하다면 clamp()와 동일한 결과를 나타냄.
*output_min(최소)과 output_max(최대)의 값이 바뀌게 되면 웨이브 자체가 뒤집어짐.
eg) @Cd = fit (sin (d), -1, 1, 0, 1); // -1에서 1의 range를 가졌던 웨이브가 0에서 1로 범위가 줄어듦. 그리고 그 결과 값은 @Cd에 store됨으로써 색깔로서 나타나지게됨.
- Built-In Attribute: @Time
@Time은 프레임이 흐를 수록 지오메트리가 움직이게 만드는 attribute이다.
eg) @Cd = fit (sin (d + @Time*0.5), -1, 1, 0, 1); // 프레임이 진행 될 수록 파형이 중심으로 모이게 되는 다이나믹한 플레이를 생성함. 수치를 곱하거나 더하여 속도를 조정 할 수 있음.
Exercises:
1. Change the direction the waves move from towards the center to away from the center
간단하게 @Time의 계산 방식을 +에서 -로 바꾸어 반대 방향으로 가게끔 설정함.
eg) @Cd = fit (sin (d - @Time*0.5), -1, 1, 0, 1);

2. Change the speed of the waves
이것 또한 간단하게 @Time에 곱하는 값을 더욱 크게 늘려 스피드를 더욱 빠르게끔 설정하였다. 그리고 스피드를 느리게 만들고 싶을땐 1보다 작은 수를 곱하여 스피드를 느리게 설정하였다. 하지만 이렇게 코드를 쓰는 것은 비효율적이라 생각하여 chf()을 이용하여 parameter로서 조정 가능하게끔 설정하였다.
eg) float speed = chf ("SPEED");
@P.y = fit(sin (d - @Time*speed), -1, 1, 0, 1);

3. Make the waves be blue on black, or *yellow on green
이것 또한 식을 담고 있는 attribute을 @P.y에서 @Cd로 바꾸어 색깔로 scene view에서 나타나지게끔 설정하였다.
eg) @Cd = 0; // @Cd의 값을 모두 0으로 초기화 함으로써 기본 배경색을 검정으로 바꿈
@Cd.b = fit(sin (d - @Time*speed), -1, 1, -1, 1); // 파란색의 웨이브가 퍼져나가는 쉐입을 구현

eg) @Cd = 0; // 전반적인 색상을 모두 0으로 초기화 해서 검정으로 만듦
@Cd.g = 1; // 초록색 배경인 grid를 만들어 초록색 바탕을 생성함
@Cd.r = fit(sin (d - @Time*speed), -1, 1, -1, 1); // 웨이브에 빨간색 attribute를 설정하여 초록색과 섞이게 만들어 노란색 웨이브를 창조하게끔 설계함

4. Rather than affect colour, make them affect the y position of the points.
우연찮게도 내가 1번과 2번에 적용하였던 쉐입이 이번 문제로 나왔다. @Cd로 store됬던 sin()이 들어 있는 식을 @P.y으로 가게끔 바꾸어 마치 파도가 일렁이는 듯한 느낌을 주는 쉐입을 형성하였다.
eg) float speed = chf ("SPEED");
@P.y = fit(sin (d - @Time*speed), -1, 1, 0, 1); // sin()웨이브가 적용된 원점과 모든 포인트들의 distance를 @P.y로 store하여 웨이브가 물리적으로 출렁이는 듯한 느낌을 구현함.
전체 VEX: (디테일한 설명은 윗 부분 (파형의 모양을 띄는 그리드를 형성하기 위한 VEX code) 에)
vector pos = @P*chv ("FANCYSCALE");
vector center = chv ("CENTER");
v@pos = pos;
float d = distance (pos, center);
d = d*chf ("SCALE");
float speed = chf ("SPEED");
@P.y = fit(sin (d - @Time*speed), -1, 1, -1, 1);

이해가 안되었던 부분:
- 3번 Exercise에 노란색 웨이브를 초록색 grid에 구현하라고 문제를 내는데 rgb만을 이용하여 노란색과 초록색을 동시에 나타내는것이 어렵게 느껴졌다. red와 green을 섞으면 노란색이 나오는 것은 이해하였지만 그렇다면 초록색 바탕을 어떻게 노란색과 grid위에 동시에 나타낼지 어려움을 느꼈다.
ps. 하지만 머리를 꽁꽁 싸맨 후에 결국 풀었다 :)
- @Time이 어떠한 방식을 통해서 전체적인 프레임이 흘러감에 따라 geometry가 다이나믹한 모션을 취하게 되는지 궁금하다.
- 전체적인 VEX code를 쓰면서 이해는 되지만 이걸 내가 스스로 전부 자신있게 쓸때까지 많은 연습이 필요할 것 같다.
공부하면서 들었던 생각:
Day 2 강의를 들어가면서 점차 VEX세계에 진정으로 입문하는 과정을 온몸으로 느끼는것 같다. 과거 코딩을 배웠지만 비주얼적으로 구현하는 후디니의 VEX는 생각보다 많이 다르고 이해하기도 생각보다는 쉽지는 않다. 중간고사 기말고사가 구두시험으로 진행된다니 코드를 완전히 이해하고 직접 쓰는데 있어 거리낌이 없도록 한줄 한줄 해석하는 능력을 키우는 것이 정말 중요할 것 같다. 특히 식이 더욱 복잡해 질 수록 천천히 보면 이해는 되지만 한눈에 딱 파악할때까지는 시간이 꽤 걸린다는 사실이 마음에 쓰인다. VEX와 완전히 친숙해 지기 까지 많은 시간이 걸릴 것 같지만 계속 이해하려고 노력하다보면 언젠가는 딱 보고 아 이렇구나 라고 이해할 수 있으면 좋겠다.