복습한 내용과 다시봤더니 이해되는 부분:
Day 1: basic assignment, component assignment, arithmetic manipulation
- Day 1때는 @P와 @Cd값들을 이용하여 특정 geometry에 vex로 영향을 주는 기본적인 식을 완성해보았다. 그리고 ch()과 sin()같은 function들을 통해 기본적인 파형을 나타내는 geometry를 생성하는 것을 배웠다.
- @P나 @ptnum이 아닌 @N (Normal)이 웨이브를 만드는 sin()이나 cos()같은 function들에게 적용되었을때 어떠한 과정을 통해 특정 쉐입을 형성하는지 궁금하다.
- Geometry Spreadsheet을 보고 각각의 수치들을 한눈에 파악하기가 어렵다.
1. @N (Normal)은 points나 primitives가 향하는 방향을 x/y/z축을 기반으로 수치를 결정한다. 내가 만약 변수를 만들어 @N 에 assign해준다면 모든 포인트에 대한 값들은 geometry spreadsheet에 display되어 유저가 모든 수치들을 표로서 볼 수 있게 한다.
2. Geometry Spreadsheet에 대한 문제는 수치를 너무 하나씩 정확하게 세부적으로 모든 포인트에 하나씩 각각 정확히 파악하기보단 이게 이렇게 되서 나타나는구나 정도로 이해하고 scene view에서 geometry가 어떠한 과정을 통해 대략 이해할 수 있으면 충분이 작업과정에 문제 없을거라 생각하고 나아가기로 하였다. 그래도 필수적인 값들의 계산들은 vex를 계속 만져보는 연습을 통해 더욱 실력을 기르기로 하였다.
Day 2: length and distance functions, animate with @Time
- Day 2때는 length()과 distance()를 사용하여 특정 포인트와 특정 포인트사이의 거리를 계산하는 방식을 알아냈고 이 function들의 특징을 이용하여 grid상에서 sin()이나 cos()를 사용하여 특정 포인트에서 은은하게 파장이 퍼져나가는 특징을 구현하는데 중점을 두었다. 또한 @Time을 통해 애니메이션을 주어보았다.
- 3번 Exercise에 노란색 웨이브를 초록색 grid에 구현하라고 문제를 내는데 rgb만을 이용하여 노란색과 초록색을 동시에 나타내는것이 어렵게 느껴졌다. red와 green을 섞으면 노란색이 나오는 것은 이해하였지만 그렇다면 초록색 바탕을 어떻게 노란색과 grid위에 동시에 나타낼지 어려움을 느꼈다.
ps. 하지만 머리를 꽁꽁 싸맨 후에 결국 풀었다 :)
- @Time이 어떠한 방식을 통해서 전체적인 프레임이 흘러감에 따라 geometry가 다이나믹한 모션을 취하게 되는지 궁금하다.
- 전체적인 VEX code를 쓰면서 이해는 되지만 이걸 내가 스스로 전부 자신있게 쓸때까지 많은 연습이 필요할 것 같다.
1. 첫번째 어려웠던 점 같은 경우는 내가 exercise를 계속 생각해보고 분석해보고 마지막에 결국 풀었던 문제였지만 다시한번 상기시켜보자면 스팅고님께서 댓글에 언급해주었던 방식처럼 @Cd = 0; 으로 배경색을 우선 모두 0으로 설정해 검정색 즉 기본값으로 초기화 시켜준다음, @Cd.g = 1;를 다시 설정해주어 전체적으로 초록색 grid를 생성시키고자 하였다. 그리고 빨강과 초록색을 섞으면 노란색으로 된다는 사실을 구글링을 통해 알아보았고 이미 초록색인 grid colour에다 빨간색 wave를 적용하면 웨이브가 적용되어 있는 부분에서는 초록색과 섞여 노란색으로 변하므로 @Cd.r = fit(sin (d - @Time*speed), -1, 1, -1, 1); 같이 특정 웨이브를 생성하는 식에 @Cd.r 즉 빨강 attribute를 저장하는 식으로 끝맺혔다.
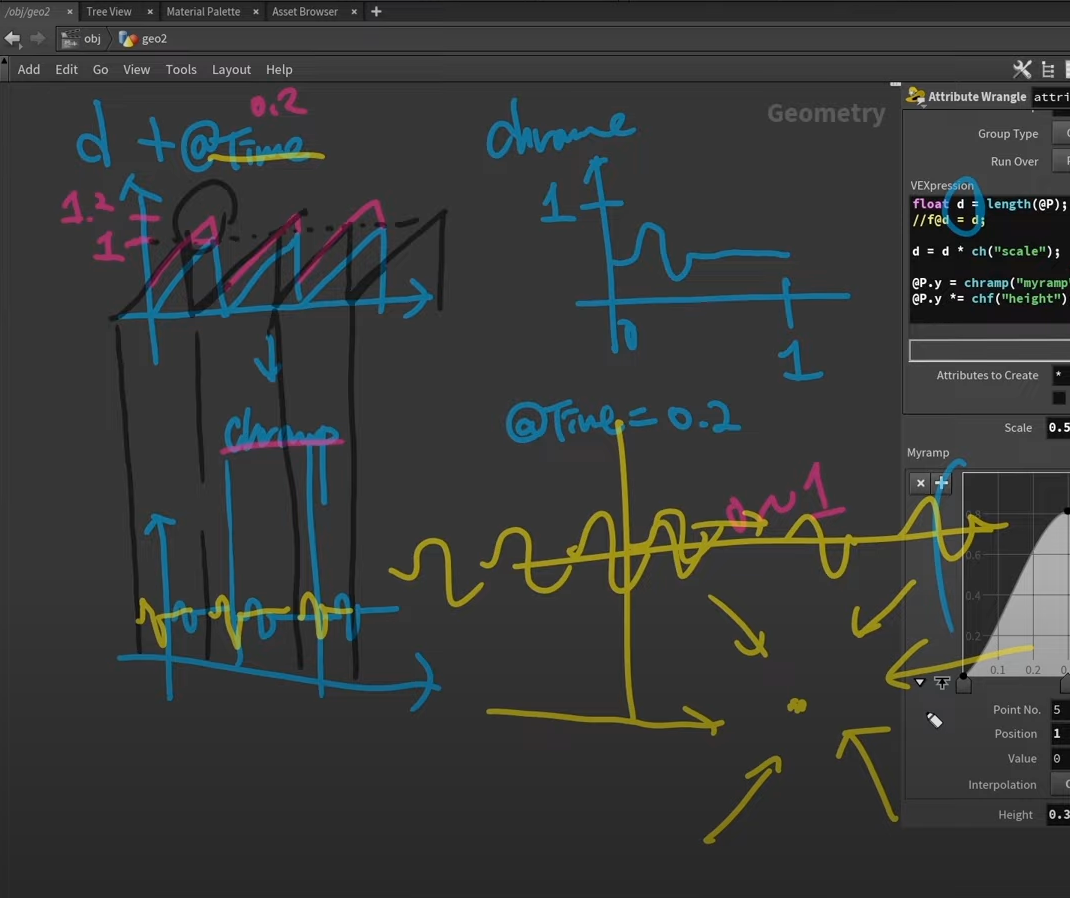
2. @Time은 결국 TWA선생님께서 Day 4때 결국 친절하게 그래프와 같이 설명해 주었던 Attribute으로써 아래의 그림과 같이 원점과 @P값 사이의 거리 길이 값에 @Time이 더해지면 ramp자체가 더욱 상승하게 되고 y값에서 0에서 1에 차지하지 않은 부분은 내림을 적용한값으로 다시 내려가 앞당겨지는 새로운 ramp를 형성하게 된다. 이게 계속 반복될수록 왼쪽으로 밀리게 되는 모션을 형성할 것이고 결국 +@Time은 파형들이 grid상에서 가장자리에서 원점으로 향하는 스타일의 모션을 구축할 것이다. 이와 반대로 @Time을 d에다 빼면 앞서 설명한 것과 비해 전부 반대로 진행되므로써 오른쪽으로 밀리게 되는 모션을 형성하여 grid 상에서 파형들이 원점에서 가장자리로 퍼지는 스타일의 모션을 만들것이다.
3. Day 4까지 오니 Day 2정도는 복습을 하였을때 다행히 이해가 쉬워보이는것 같다...ㅋㅋㅋ 이때는 새 발의 피였던것 같다.
Day 3: clamp and fit, waves
- 우선 Day 3의 시작은 Day 1때 자세히 다루어지지 않은 @N을 제대로 소개함으로써 문을 열었다. @N은 포인트와 프리미티브가 향하는 방향을 수칫값으로 나타내는 역할을 하며 이로인해 입체적인 geometry를 표면적으로 ramp즉 웨이브를 적용할 수 있는 것을 알 수 있었다. (아래 토미 사진처럼). 또한 clamp()와 fit()을 통해 특정 파형에 모양을 조절하는데 배웠다. fit()은 기본적으로 세번째 인풋까지 clamp()의 인풋과 동일한 사실을 안후 두 function들이 밀접한 관계를 맺고 있다는 사실을 알 수 있었고, clamp()는 range값을 넘어가는 모든 파형의 값들을 최솟값과 최댒값까지 제한한채 아예 납작하게 눌러버리는 특징을 알 수 있었고, fit()은 이렇게 조절된 ramp를 range의 맞춰서 확대 또는 축소의 원리를 작동시킨다는 사실을 배울 수 있었다.
- fit function이 대강 이해는 되어가지만 더욱 geometry가 복잡해지고 grid가 아닌 보다 입체적인 오브젝트를 다룰때 많이 햇갈릴 것 같다는 예감이 든다. 특히 fit function을 물리적인 웨이브나 쉐입의 높낮이나 한눈으로 관찰 할 수 있는 @P같은 Attribute들로 지정할때는 딱 한눈에 보여 어떤 느낌인지 이해가 가는것이 쉽지만 @Cd같이 물리적으로 한눈에 파악할 수 없는 Attribute에 fit function을 적용할때는 많이 햇갈리는 부분이 있다. 예를 들어 @Cd = fit (input, inmin, inmax, outmin, outmax); 같은 부분은 생각만해도 머리가 터질것 같다는 느낌을 받을 것 같다.
- 코드가 복잡해지면서 점점 햇갈려지는 비중이 커지는것 같다.
1. TWA님께서 말씀하신것: 일단 솔직히 말해서 이런 부분이 절대량과 관련이 있는 데 많이 상황을 마주치고 겪어보면서 감을 길러야한다. @Cd를 효과 제작과정에서 쓰는 이유는 과연 내가 주려는 효과가 어디에 어떻게 얼마나 세게 적용되는지 확인하고 싶어서 그런경우가 많다. 예를들어 어떤 vector 변수 K가 있다 했을때 K가 @P 각각의 위치 정보에 어떻게 영향을 줄 수 있을까 확인하기 위해 @Cd = @K; 이런식으로 확인 할 수 있다.

2. TWA선생님 왈: 이제 곧 머리속이 엉망진창이 될텐데 즐기시길 바란다 원래 고통스럽다...
...ㅋㅋㅋ.... 고통을 즐기겠습니다....ㅋㅋ
Day 4: chramp, using on attrib components, on time, on reranging outputs
- Day 4에서는 chramp()을 통해 직접 유저가 ramp의 모양을 그릴 수 있다는 사실을 배웠다. 그리고 가장 중요한 것으로써 이 chramp()가 sin()값이 기본적인 웨이브에 적용되었을때 특정 과정을 통해 모양이 유저가 만든 ramp와 다른 양상을 띈 즉 새로운 형태의 웨이브를 형성하는 사실을 알 수 있었다. (자세한건 아래 2번 설명 참조). 그리고 @Time이 어떠한 과정을 통해 흐르는 방향이 결정되는지 배웠다. (Day 2부분 설명 2참조).
- 무엇보다도 d값에 @Time이 더하거나 빼질때의 경우를 배우는데 있어서 그래프로 이해하는데 많은 어려움을 느꼈다. 원점과 포인트 위치 사이의 거리길이에서 @Time을 더해주면 왜 grid상에서 원점으로 흘러가는 모션이 취해지는지, 그리고 그 반대는 또 왜 퍼져 나가는지 이해하기가 힘들었던것 같다. 이 부분에서 시간을 제일 많이 소요했던것 같기도 하다.
- sin()과 chramp()의 관계는 마지막에 결국 이해를 하였지만 이것도 시간을 꽤 많이 잡아먹은 부분중 하나였던것 같다... 후반강의에서 멘탈이 나가버린 나를 발견할 수 있었던것 같다...
- 항상 말했듯이 코드가 많아지고 복잡해 짐에따라 머리가 터져나갈것 같다... 계속 tweak도 해보고 뭐 다 해보고 있다. 주말에 짬날 때 생각보다 vex를 스스로 많이 다뤄보아야 겠다는 생각이 들고있다.
1. 이 부분은 Day 2 두번째 이해 안되었던 부분에서 언급한 똑같은 개념이다. 자세한건 그 부분을 올려서 봐야겠다. 솔직히 말해서 이 부분이 제일 막혔던 것 같다.
2. sin()과 chramp()의 관계는 결론적으로 sin()의 세로 즉 y값이 chramp()에서 가로즉 x값으로 으로 진행되어 나간다고 이해하니 더욱 편했다. 이 부분은 말로 설명하기는 힘든 부분이 있어 Day 4때 첨부하였던 사진을 여기다 올리겠다.
3. 뭐든지 연습...
다시봐도 모르겠는 부분:
- 앞서 언급했듯이 솔직히 말해서 Day 4 중후반쯤 강의 에서 배운 d 에 @Time이 더해졌을때와 빼졌을때에 방향이 어떻게 설정되었는지 아직도 아리송한 부분이 있다. 나머지는 강의를 반복해서 들으며 어느정도 이제 감을 확실히 잡은것 같지만 이 부분은 친절하게 그래프상으로 설명을 해주심에 있어 내 뇌로는 완전히 정복하지 못한것 같다...ㅠ
- vex를 통해 여러 응용을 해봐야 할 것같다. 실력을 향상시키기 위해 더욱 창의적인 모션, 이펙트를 주기위한 많은 실험을 해봐야 한다는 것을 요즘 많이 느끼고 있다.
- 레고 만들기 프로젝트 기대된다. 내일부터 주말동안 시도해 볼 것이다. 오랜만에 최초입문강의때 배웠던 스킬들을 발휘할 예정이다. 막히면 twa선생님의 영상을 보고 참조도 할 것 같다. 내가 배우지 않았던 새로운 이론이나 feature들이 해답 튜토리얼 영상에 나올지는 확실치 않지만 최대한 최선을 다해 레고와 비슷하게 만들 것이다.