중요했던 부분:
- chramp(): Channel Ramp Function
스팅고님 일기에서:
@P.y = chramp ("TWA", K); // 변수 K값을 이용하여 @P.y에 적용하세요라는 의미이다.
ch()의 파라미터처럼 유저가 직접 인터페이스를 통해 파형을 직접 그릴 수 있게하는 function. 직접 파형 (정확히는 ramp) 쉐입을 그릴수 있는 파라미터를 생성하는 function.
보통은 그래프 모양으로 유저가 조정할 수 있게끔 설계되어있으며 y와 x축을 기반으로 파형의 형태를 그릴 수 있게끔 한다.

eg) @P.y = chramp ("TWARAMP", @P.y); // @P.y attribute에 해당하는 파형을 직접 그릴 수 있게 하는 parameter를 생성하여라. chramp()에 있는 모양을 만들어 줌으로써 각각에 대응되는 정보가 @P.y 높이값으로써 저장이 되어있는 것을 알 수 있다.
*그 중 인터페이스 안에 유저가 세팅할 수 있는 파라미터들이 몇개 있는데...
position - 파형을 이루는 점의 x축 위치
value - 파형을 이루는 점의 y축 위치
Interpolation - 점들 사이에 있는 정보들이 어떻게 배열될 지 보는 것
- Linear: 값이 서서히 증가하는 방식
- Constant: 점들 사이에 있는 정보들이 다음 점을 만나기 전까지 그 전에 있던 점의 정보를 유지하는 방식
- Catmull-Room: 값이 서서히 증가하지만 곡선형태로 부드럽게 점들과 이어지는 방식
- Bezier: 점의 위치를 기준으로 ramp를 끌어당겨 곡선의 정도를 조절하는 방식
eg) float d = length (@P); // 모든 포인트와 원점 사이의 거리를 float variable d에다 저장
f@d = d; // display every data of the float variable d in the geometry spreadsheet
d = d*ch ("SCALE"); // d값의 스케일을 조정할 수 있음. 거리값에 상수를 곱하면 0을 제외하고 양수로 늘어남
// @P.y = d; // chramp방식을 적용하지 않은 식, 원래는 원점을 중심으로 솟아 올라가는 깔대기 모양을 예상함
@P.y = chramp ("YRAMP", d); // chramp방식을 적용한 식, 원점을 중심으로 올라가다가 다시 내려가고 또 올라가는 형태가 반복되는 형태로 나타나기 시작함. 그리고 나는 chramp()의 parameter에 있는 ramp 그래프는 정확히 0에서 1까지의 구간까지만을 의미하는 것을 알기 시작했고 이 구간보다 큰 값을 (예 - 이 식에는 @P.y) 가진 geometry는 ramp가 반복되는 형태로 나타나진다는 사실을 깨달음.
@P.y = @P.y * chf ("HEIGHT"); // chramp()을 적용하고 나서 ch()으로써 @P.y을 곱한 값을 @P.y에 저장한다면 패턴의 높이값이 늘어나거나 줄어들게 조정 할 수 있음.
특징:
- chramp()는 input으로 들어오는 값을 0과 1 사이의 값으로 변환을 한다. 0에서 1, 1에서 2, 2에서 3 이든 관계없이 0에서 1사이의 값으로 싹다 변환한다.
- 윗 코드 처럼 float d = length (@P); 를 이용해서 만든 chramp()는 음수에 있는 포인트들과 원점사이의 거리길이를 모두 다 양수로 바꿔주기 때문에 음수의 거리길이는 불가능함으로 원점을 중심로 대칭된 쉐입을 만든다.
- 내가 만든 SCALE 파라미터를 올린다 하들 chramp()에 의해 @P.y값이 1까지 제한되므로 (본래는 0을 제외한 @P.y가 모두 위로 상승함) y=nx 방식처럼 경사면만 가파라진체 패턴이 더욱 촘촘해진다. 반대로 줄이면 느슨해지는 패턴을 만든다.
- 그치만 HEIGHT 파라미터를 통해 이미 chramp()값이 적용된 패턴에 geometry자체에 @P.y값 (높이값)을 조정할 수 있는 기회가 생기므로 geometry의 높이를 높게 아니면 줄어들게 만들 수 있다.
Tip: chramp()에 있는 패턴이 계속 반복되어 나타나는 형태로써 geometry에 나타나므로 chramp()의 ramp를 구성하는 점들 중 첫번째 값과 마지막 값이 동일한게 더욱 자연스러운 패턴을 준다.


- Clip (Direction)
geometry의 단면을 쪼개는 노드. 파라미터중 Direction은 단면을 짜르는 방향을 나타내는 것 같다.
- @Time과 @chramp의 관계
오늘 강의 생각보다 쉬운데...? 한건 실수였다. 여기서부터 머리가 하얗게 되버린것 같다.

eg) d = d + @Time;
// 우선 원점으로부터 거리값 (d)에 @Time (@Time이 0.2라 가정했을때)을 더하면 그래프에서 ramp가 0.2씩 올라간다. 그렇지만 그렇게 된다면 0에서 1까지의 구간에 ramp가 0.2만큼 튀어 나와있는 것을 알 수 있다. 그러면 이 부분이 다시 그래프 상에서 아래로 옮겨지게 된다. 이런 상태로 ramp를 다시 그리면 파형이 앞당겨지는 형태의 ramp pattern을 확인 할 수 가 있다. 그렇게 되면 chramp()에서 직접 그린 ramp도 d 그래프에 형성된 ramp를 따라 같이 앞당겨지는 형태의 패턴을 형성하게 되어 그게 반복되어 마치 ramp가 반대로 원점으로 향하는 모션을 취할수 있게된다.
binart.p님께서 말하신 것 - Chramp input이 0-1까지만 나와서 +@Time 하다보면 chramp가 값을 다시 변환해서 계산하다보니 그래프가 왼쪽으로 밀리는 애니메이션이 될것이다.
그러므로
eg) d = d - @Time;
// 스팅고님께서 말하신 것 - 같은 식을 준다면 반대로 원점으로부터 멀어지는 파형이 생긴다. 또한 이것이 가능한 이유는 앞서 말했듯이 d가 length 거리값이라서 음수에 있는 포인트들이 양수의 절댓값으로 바뀌므로 대칭을 띄어서이다.
솔직히 이 부분은 너무 어렵다. 주말에 계속 이 부분은 반복해서 들어야 할 것같다... 내가 쓰면서도 확 와닿지 않는것이 조금 불안하다...
- d (원점으로부터의 거리길이)를 sin()값으로 집어넣고나서 chramp()를 적용하였을때에
eg) cgwiki가 제공한 코드:
float d = length (@P);
d *= ch ("SCALE");
d += @Time;
d = sin (d); // 추가된 코드. chramp()를 적용하기전 d에 sine 패턴을 적용함
d = fit (d, -1, 1, 0, 1); // fit function을 이용해 -1에서 1까지의 결과를 0에서 1까지로 지정해준다.
// @P.y = d; // 여기까지의 식으로만 보면 sine function만 적용된 곡선 파형이 나옴. 특히 음수의 위치에 있는 포인트들은 절댓값으로 수치가 변하여 대칭적인 구조를 이루게됨.

@P.y = chramp ("MYRAMP", d); // chramp()을 새롭게 지정하여 위에 형성된 곡선 모양의 파형에 유저가 직접 그린 ramp를 다시 적용하였을때
@P.y *= ch ("HEIGHT"); // 유저가 직접 높잇값을 조정할 수 있게 만듦


그렇다면 이 형태의 파형은 어떻게 만들어 졌을까? 왜 내가 만든 형태의 chramp()의 ramp와 다르게 나올까? sine wave가 어떠한 방식으로 내 ramp에 영향을 줄것일까? 이것에 대해 많은 고찰이 필요하였다.

유튜브 댓글 중: "d 값이 sin그래프 일 때, 결과 그래프를 chramp 그래프의 뒤 부터 읽고 나타내주셨는데요. 그 이유가 d가 @P.y 값이기 때문에, d 그래프 에서 첫 시작점인 0.5-> 1 / 1-> 0.5 이 지점의 y 값이 chramp 그래프의 x값이어서 뒤 부터 읽고 나타내 주신 게 맞을까요..? 그리고 데칼코마니의 형태처럼 결과 값이 나오는 이유는 length 펑션 때문이구요..!" 이 해석이 내 이해에 많은 도움이 되었던것 같다.
TWA: "핵심은 0에서 1사이의 값을 그림으로 함수치환이 가능하다는 부분이에요!!!"
나는 이것은 d가 @P.y로서 지정되었기 때문에 왼쪽 그래프에서 y 즉 세로값이 오른쪽 파형의 x 즉 흘러가는 위치를 의미한다고 생각하면 이해하기 쉽다고 생각했다. 말로는 설명하기는 힘든 부분이 있다. 그치만 이 부분은 반복적으로 이해하려고 노력한 끝에 감은 잡은것 같다.
Exercises:
1. Create sawtooth waves, triangle waves, square waves
나는 여려 형태의 웨이브를 만들기 위해 간단하게 chramp() 기본값을 적용시키기로 하였다.
VEX I have written:
@P.y = chramp ("TWA", @P.x*chf ("RAMPSCALE")); // 간단하게 한줄 식을 사용하였다. length()를 사용하여 새로운 variable d 에 집어넣지 않은 이유는 음수의 거리 길이로 인한 절댓값을 피하기 위함이었다. 그러므로인해 데칼코마니 같은 모양의 웨이브를 피할 수 있었다. 또한 @P.x 값에 chf()을 곱하여 간격을 조정할 수 있게끔 설정 하였다.
Sawtooth:

Triangle:
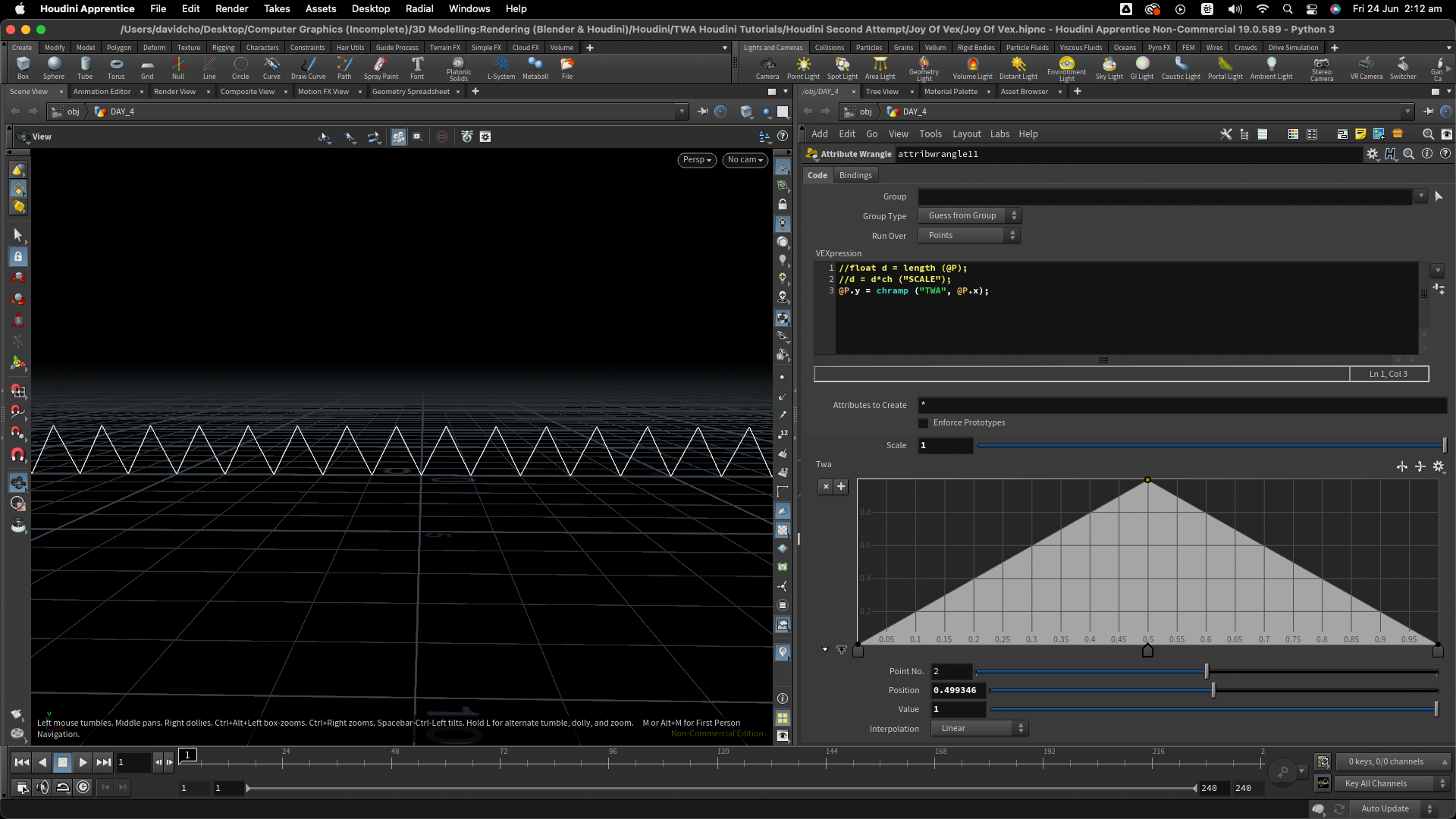
Square:

2. Affect colour in this way to make a shape pulse with pleasing colours
VEX I have written:
@P.x += @Time; // @P.x 자체에 @Time을 더하여 계속 흐르게끔 모션을 취하도록 유도하였다
@P.y = chramp ("TWA", @P.x*chf("RAMPSCALE")); // @P.y 높이값에 chramp()을 적용하여 본격적인 쉐입을 주었고 @P.x에 곱해진 ch()을 통해 램프의 간격을 조절할 수 있게끔 세팅하였다.
@P.y *= chf ("HEIGHT"); // 그후 @P.y에 ch()을 곱하여 높이값을 조절할수 있게끔 세팅하였다.
// 여기서부턴 내가 맘에 드는 색깔이 나올때까지 계속 tweak한 식들이다.
@Cd.r = chf ("RED");
@Cd.g = chf ("GREEN");
@Cd.b = chf ("BLUE");
@Cd = 1;
@Cd.r = sin(@P.x);
@Cd.g = cos(@P.x);
@Cd.b = sin(cos(@P.y));
3. Do this to the different colour components at the different rates, get trippy
이번엔 grid와 tommy를 활용하여 더욱 화려하게 만들었다. 그리고 코드 방식들도 바꿔보았다.
VEX I have written:
float d = length (@P); // 원점으로부터 @P까지의 거리
d *= chf ("SCALE"); // SCALE을 조종하여 ramp의 간격설정
d -= @Time; // 퍼져나가는 느낌의 모션 작동
@P = @P + @N*chramp ("TWA", d*chf("RAMPSCALE")); // chramp()을 사용하여 화려한 느낌을 구현하였다. 그리고 Normal attribute를 통해 표면적으로 울통불퉁 나오게끔 설정하였다.
d *= chf ("HEIGHT"); // 파형 높이값 설정
// 여기서부턴 내가 tweak 해본 @Cd 값들
@Cd = 0;
@Cd.r = sin(d*@Time);
@Cd.g = cos(d*@Time);
@Cd.b = sin(d*@Time)*cos(d*@Time);
4. Affect colour and position in different ways, find the most interesting way to break the pig. Keep all the effects controllable from channels.
VEX I have written:
// 윗 코드와 거의 동일하지만 색깔을 여러번 시도하여 약간 다르게 tweak 해보고 무엇보다 chramp()의 파라미터들을 여러번 tweak 해보아 보았다. 그리고 대부분의 parameter들은 chramp()을 통해 조정이 가능하게끔 만들었다.
float d = length (@P);
d *= chf ("SCALE");
d -= @Time;
@P = @P + @N*chramp ("TWA", d*chf("RAMPSCALE"));
d *= chf ("HEIGHT");
@Cd = 0;
@Cd.r = sin(@Time);
@Cd.g = cos(@Time);
@Cd.b = sin(d*@Time)*cos(d*@Time);
이해가 안되었던 부분:
- 무엇보다도 d값에 @Time이 더하거나 빼질때의 경우를 배우는데 있어서 그래프로 이해하는데 많은 어려움을 느꼈다. 원점과 포인트 위치 사이의 거리길이에서 @Time을 더해주면 왜 grid상에서 원점으로 흘러가는 모션이 취해지는지, 그리고 그 반대는 또 왜 퍼져 나가는지 이해하기가 힘들었던것 같다. 이 부분에서 시간을 제일 많이 소요했던것 같기도 하다.
- sin()과 chramp()의 관계는 마지막에 결국 이해를 하였지만 이것도 시간을 꽤 많이 잡아먹은 부분중 하나였던것 같다... 후반강의에서 멘탈이 나가버린 나를 발견할 수 있었던것 같다...
- 항상 말했듯이 코드가 많아지고 복잡해 짐에따라 머리가 터져나갈것 같다... 계속 tweak도 해보고 뭐 다 해보고 있다. 주말에 짬날 때 생각보다 vex를 스스로 많이 다뤄보아야 겠다는 생각이 들고있다.
공부하면서 들었던 생각:
솔직히 Joy of Vex는 스터디 그룹 전 7일차까지 들어본 경험이 있다. 하지만 바빴던 대학교 학기가 끝나고 지금와서 첨부터 들으니 생각보다 내가 많이 까먹은것에 있고 심지어 햇갈려하는 부분에 있어서 조금 충격을 먹고 있다. 그리고 안 사실은 이것은 손을 놔버리면 다시 문외한이 될것이라는 것이었다. 계속 만져보고 감각을 익혀보고 완전히 내껏으로 만들어야 겠다는 사실이 기정사실화로 다가오는것 같다. 생각보다 호락호락하지 않다... 분명 3시간 이하정도면 공부량 충분하겠지 했는데... 강의 후반부분에 이해를 못해서 그런지 3시간은 커녕 5시간은 강의를 계속 반복해서 들어보는데 쓴것같다... 근데 아직 4일차다... 내가 알기론 7일차는 포기하기 좋은 코스라고 들었다.... 그치만 포기는 안할거다. 인생에 쉬운것은 없는것 같다... 이제부터는 악으로 깡으로 버텨야겠다...